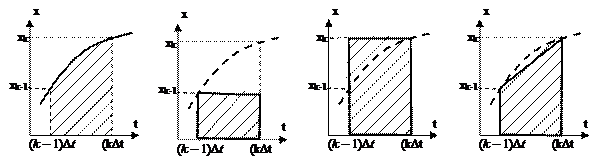Для формирования массивов выходных переменных структура FormulaNodeпомещается внутрь структуры ForLoop, при этом задержанные на интервал дискретизации отсчеты выходных переменных y ₁ и v ₁ получаются с помощью регистра сдвига (рис.3).

Прямой метод Эйлера при большом интервале дискретизации может дать неустойчивое решение. Это случится, если отклонение решения от входного процесса x_{k - 1} - y_{k - 1} (см формулу (5)) даст такое значение y_k . что отклонение на следующем шаге x_k - y_k будет той же величины, что и предыдущее, но обратным по знаку. Решение будет колебательным незатухающим.

К графическому индикатору

Рис.4

В предыдущих лабораторных работах развертка графического индикатора Graphосуществлялась автоматически в соответствии с типом данных, подаваемых на вход графического индикатора. В этой работе мы сформируем данные так, чтобы по горизонтальной оси откладывалось время. Для этого надо сформировать кластер, куда кроме массива данных будет входить информация о времени. Используем ВП Bundle (Объединить), который находится в подпалитре Cluster (Кластер). На его входы elementподаются (см. рис.4): на верхний - время начала развертки - 0; на средний - интервал дискретизации - Δt; на нижний - массив данных

Замена непрерывной передаточной функции дискретной

Если математическая модель системы представляется в виде соединения линейных и нелинейных блоков, то для описания линейных блоков чаще всего используется передаточная функция K (p ). В этом случае цифровую модель непрерывного линейного блока можно получить, заменив непрерывную передаточную функцию K (p ) дискретной K (z ).

Для этого можно использовать связь между непрерывными и дискретными изображениями, устанавливаемую дискретным преобразованием Лапласа (Z -преобразованием). В таблице 1 приведена эта связь для передаточных функций, используемых в данной лабораторной работе.

Таблица 1

K (p )	1 p	1 p 2	1 (1 +pT )
K (z )	Δt z (z - 1)	(Δt ) 2 z (z - 1) 2	(Δt /T ) z (z - e- Δt /T )

Заметим, что здесь комплексная переменная z определяется как z = e^{p Δt} и является оператором опережения на интервал дискретизации. Соответственно z ^-1 - это оператор задержки на интервал дискретизации.

Другой путь предусматривает непосредственный переход от комплексной переменной p к комплексной переменной z заменой операции аналогового интегрирования 1/p операцией дискретного интегрирования. При дискретном описании аналогового интегрирования можно оперировать только с значениями входного и выходного процессов в моменты дискретизации. На рис.5 показано, как это можно сделать, используя численное интегрирование по методу прямоугольников и по методу трапеций.

Значение выходного процесса y_k интегратора в момент времени t= k Δt отличается от предыдущего значения y_{k -1} на величину площади S под кривой x (t ) (заштрихованная фигура на рис.5 а ).

yk = yk- 1 + S	yk = yk-1 + Δt xk-1	yk = yk- 1 + Δt xk	yk = yk - 1 + +Δt (xk + xk - 1 ) /2
а )	б )	в )	г )
Рис.5

По методу прямоугольников площадь можно определить по разному в зависимости от того, какую величину принять за высоту прямоугольника: x_{k - 1} или x_k (рис.5.5 б и рис.5.5 в ). На рис.5.5 г ) показано, как вычисляется эта площадь по методу трапеций. Рекуррентные формулы для интегрирования приведены под рисунками.

По этим формулам можно записать дискретные передаточные функции. Поясним это на примере интегрирования по методу трапеций:

y_k = y_{k - 1} + Δt (x_k + x_{k - 1} ) /2.

Перенесем y_{k - 1} в левую часть и возьмем от полученного выражения Z -преобразование. Учитывая, что запаздывание на интервал дискретизации в области оригиналов соответствует умножению на z ^-1 в области изображений, получим:

Y (z ) - z^{- 1} Y (z ) = (Δt /2) (X (z ) + z^{- 1} X (z )).

Дискретная передаточная функция - это отношение Z -изображений выходной и входной переменных, поэтому

K (z ) = Y (z ) /X (z ) = (Δt /2) (1 + z ^-1 ) / (1 - z ^-1 ) = (Δt /2) (z + 1) / (z - 1).

В таблице 2 приведены выражения дискретных передаточных функций для различных методов численного интегрирования для одного и двух интеграторов.

Таблица 2

K (p )	K (z )
	Метод прямоугольников (1)	Метод прямоугольников (2)	Метод трапеций
1 p	Δt z - 1	Δt z z - 1	Δt (z + 1) 2 (z - 1)
« 1 2 3 4 5 6 » К-во Просмотров: 293 Бесплатно скачать Реферат: Моделирование линейных непрерывных систем в среде LabVIEW >>> Скачать <<< Меню Поиск