Реферат: Моделирование линейных непрерывных систем в среде LabVIEW

К

р (1 + рТ )

К_р (р ) =. (10)

Такая модель часто используется при анализе ошибок в следящей системе.

Запишем дискретную передаточную функцию разомкнутой системы, заменяя интеграторы по методу прямоугольников (2). Для этого преобразуем передаточную функцию разомкнутой системы (5.10), поделив числитель и знаменатель на р ² :

К /р 2 Т + 1/р

К_р (р ) =.

Используя соотношения, приведенные в таблице (5.2), получим:

К (Δt )2 z /(z – 1)2 Т + Δt z /(z – 1)

b1 z z2 + a1 z + a2

К_р (z ) = =, (11)

где b ₁ = K (Δt ) ² / (T+ Δt ), a ₁ = - (2T+ Δt ) / (T+ Δt ), a ₂ = T / (T+ Δt ).

Для моделирования устройства с передаточной функцией (11) используется БИХ-фильтр, коэффициенты числителя которого (ForwardCoefficients) представляются массивом из двух элементов (0,b ₁ ), а коэффициенты знаменателя - массивом из трех элементов (1, a ₁ ,a ₂ ).

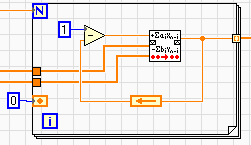
Специфика использования БИХ-фильтра заключается в том, что неизвестен целиком входной массив Х , а известен только текущий элемент, а следующий элемент рассчитывается с учетом значения текущего элемента выходного массива фильтра. В LabVIEWсуществует такой фильтр - IIRFilterPtByPt (IIRFilterPointByPoint - БИХ-фильтр точка за точкой).

Рис.6

Вычисления БИХ-фильтром IIRFilterPtByPtпроизводятся в цикле For

Loop (рис.5.6). В этом же цикле генерируется единичное входное воздействие. Автоматическое появление в цепи обратной связи регистра сдвига обусловлено тем, что рассчитанное значение выходного процесса используется для сравнения с входным только в следующем интервале дискретизации, то есть с запаздыванием на интервал дискретизации. В результате вычислений формируется массив переходной характеристики.

Для точного расчета переходной характеристики воспользуемся ВП ODELinearnthOrderNumeric - “Решение линейного обыкновенного дифференциального уравнения n-го порядка в численном виде” (рис.7).

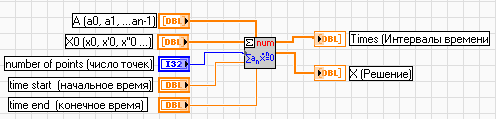Рис.7

ВП находит решение в виде суммы экспонент и вычисляет его для заданных точек. Поэтому решение точное.

Вход А представляет собой массив коэффициентов дифференциального уравнения в порядке увеличения степени производной. Коэффициент при производной самой высокой степени считается равным 1 и не требует ввода.

На вход Х0 подается массив начальных условий - начальные значения решения и его n - 1 - й производных.

Вход “число точек" задает число равноудаленных по времени точек между начальным и конечным временем

Выход Х содержит массив значений решения в равномерно расположенных по оси времени точках. Значение времени в этих точках выводится в массиве Times.

Дифференциальное уравнение замкнутой системы запишем по передаточной функции замкнутой системы:

Кр (р) 1 + Кр (р )

К Тр2 + р + К