Реферат: Моделирование продажной стоимости двухкамерного холодильника
Получаем следующие оценки коэффициентов регрессии методом наименьших квадратов:
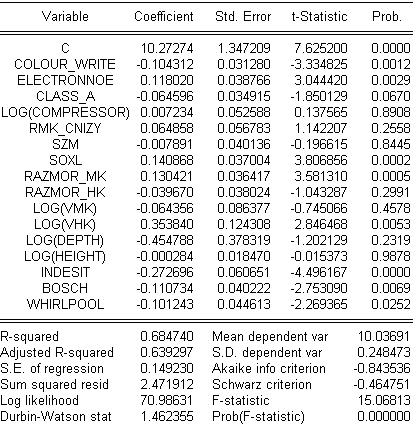
Рис. 5.3.1. Результаты оценивания объясняющих переменных и модели в целом
При 5-типроцентномуровнезначимостиследующиекоэффициентыоказалисьнезначимыми: class_a, log(compressor), rmk_cnizy, szm, razmor_hk, log(vmk), log(depth), log(height).
Модель в целом значима, доля общей вариации результирующего признака составила 0,6847.
С целью исключения коррелирующих между собой факторов рассмотрим корреляционную матрицу (Приложение 3).
В результате последовательного исключения незначимых переменных получили следующие результаты оценивания:
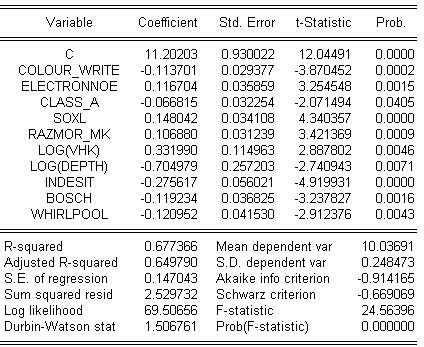
Рис. 5.3.2. Результаты вычисления после исключения незначимых переменных
LOG(PRICE) = 11.2020286 - 0.1137005911*COLOUR_WRITE + 0.1167036723*ELECTRONNOE - 0.066814893*CLASS_A + 0.1480422557*SOXL + 0.106879945*RAZMOR_MK + 0.3319897268*LOG(VHK) - 0.70497857*LOG(DEPTH) - 0.2756174193*INDESIT - 0.1192342258*BOSCH - 0.1209517658*WHIRLPOOL
Модель в целом осталась значима; доля общей вариации результирующего признака уменьшилась на 0,0073 и составила 0,6774.
Для исследования полученной модели на наличие гомоскедастичности используется тест Уайта:

Рис. 5.3.3. Результаты теста Уайта
На 5% уровне значимости, гипотеза о гомоскедастичности принимается.
Проводим RESET-тест на ошибку спецификации регрессоров:

Рис. 5.3.4. Результаты RESET-теста
Результат RESET-теста свидетельствует об отсутствии ошибки спецификации.
5.4 Выбор наилучшей модели
В процессе моделирования получено две значимых модели, качественно описывающих процесс формирования на рынке г. Челябинска продажной стоимости двухкамерных холодильников.
Так как линейная модель имеет ошибочную спецификацию, то сразу перейдем к рассмотрению логарифмической и полулогарифмической модели.
Для сравнения логарифмической и полулогарифмической модели воспользуемся J-тестом, для этого составим прогноз цены для логарифмической модели (LPRICEF) и прогноз цены для полулогарифмической модели (PRICEFL). Затем построим следующие регрессии:
Для полулогарифмической:
LOG(PRICE) = C(1) + C(2)*COLOUR_WRITE + C(3)*ELECTRONNOE + C(4)*CLASS_A + C(5)*SOXL + C(6)*RAZMOR_MK + C(7)*VHK + C(8)*DEPTH + C(9)*INDESIT + C(10)*BOSCH + C(11)*WHIRLPOOL + C(12)*LPRICEF
Длялогарифмической:
LOG(PRICE) = C(1) + C(2)*COLOUR_WRITE + C(3)*ELECTRONNOE + C(4)*CLASS_A + C(5)*SOXL + C(6)*RAZMOR_MK + C(7)*LOG(VHK) + C(8)*LOG(DEPTH) + C(9)*INDESIT + C(10)*BOSCH + C(11)*WHIRLPOOL + C(12)*PRICEFL
При проведении сравнения между полулогарифмической и логарифмической моделями посредством применения J-теста получены следующие результаты:
Для полулогарифмической модели: