Реферат: Моделирование продажной стоимости двухкамерного холодильника
Рис. 5.4.1 Результаты J-теста для полулогарифмической модели
Для логарифмической модели:
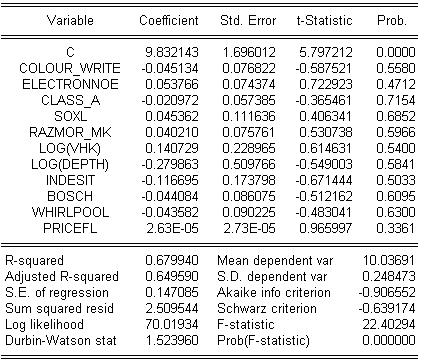
Рис. 5.4.1 Результаты J-теста для логарифмической модели
Получаем, что при 5-и процентном уровне значимости нулевая гипотеза полулогарифмической регрессии принимается, поскольку коэффициент при LCENAF =3,54Е-05 и Probability равна 0,2373, то есть этот коэффициент в полулогарифмической модели незначим. В логарифмической модели нулевая гипотеза также принимается, так как коэффициент при CENAFL =2.63E-05 и Probability равна 0,3361. Следовательно, обе модели принимаются.
Для выбора лучшей модели проверим логарифмическую и полулогарифмическую модели на соответствие теоретической цены реальной. Для полулогарифмической модели точность прогноза для контрольной выборки составляет 89,01%, а для логарифмической 88,41%. Получаем, что полулогарифмическая модель более точна. Поэтому выберем ее как итоговую модель.
6. Проверка качества модели
Рассмотрим полученную итоговую модель:
LOG(PRICE)= 10.4865 -0.1133*COLOUR_WRITE +0.1166*ELECTRONNOE -
(0,225) (0,029) (0,035)
0.0673*CLASS_A + 0.1475*SOXL + 0.1076*RAZMOR_MK + 0.0015*VHK -
(0,032) (0,034) (0,031) (0,0005)
0.0117*DEPTH -0.2759*INDESIT -0.1186*BOSCH -0.1224*WHIRLPOOL
(0,0 04 ) (0,0 56 ) (0,0 36 ) (0.042)
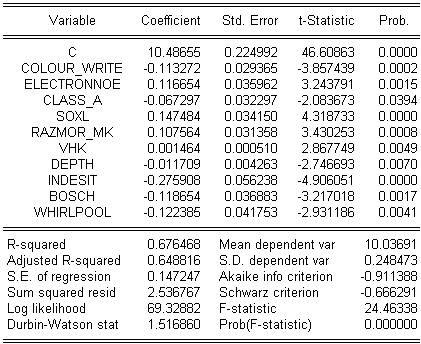
6.1. Значимость коэффициентов регрессии
Для определения значимости коэффициентов регрессии необходимо определить фактическое и критическое значение t-критерия Стьюдента при определённом уровне значимости, если | t | > tкр , то гипотеза о незначимости коэффициента отвергается. Фактическое значение t-статистики рассчитывается, как частное оценки коэффициента и стандартной ошибки оценки.
В нашем случае, на этапе устранения мультиколлинеарности из всех трех моделей были исключены незначимые переменные, после чего были построены модели, содержащие исключительно значимые переменные.
6.2 Значимость модели в целом
Коэффициент R-squared = 0.676468 говорит нам о хорошем качестве подгонки регрессионной модели к значениям выборки. AdjustedR- squared = 0.648816 также утверждает о соответствии модели.
6.3 Соответствие модели выборочным данным
Проверим близость реальных данных модельным, полученным по контрольной части выборки:
Таблица 6.3.
Близость прогнозирования
| № п/п | Наблюдаемая цена | Прогноз | Отклонение прогноза | Ошибка прогноза (%) |
| 1 | 16750 | 17894,55 | 1145 | 6,83% |
| 2 | 19790 | 20314,06 | 524 | 2,65% |
| 3 | 17550 | 15590,47 | -1960 | 11,17% |
| 4 | 23330 | 25906,46 | 2576 | 11,04% |
| 5 | 25600 | 21008,44 | -4592 | 17,94% |
| 6 | 20462 | 20410,32 | -52 | 0,25% |
| 7 | 15450 | 17447,8 | 1998 | 12,93% |
| 8 | 17750 | 25580,35 | 7830 | 44,11% |
| 9 | 34450 | 30624,34 | -3826 | 11,10% |
| 10 | 30500 | 30732,64 | 233 | 0,76% |
| 11 | 23550 | 25734,23 | 2184 | 9,27% |
| 12 | 34800 | 30710,11 | -4090 | 11,75% |
| 13 | 27700 | 22194,84 | -5505 | 19,87% |
| 14 | 29873 | 29950,12 | 77 | 0,26% |
| 15 | 24125 | 23448,77 | -676 | 2,80% |
| 16 | 19490 | 25047,39 | 5557 | 28,51% |
| 17 | 25930 | 23310,13 | -2620 | 10,10% |
| 18 | 32659 | 31647,86 | -1011 | 3,10% |
| 19 | 31400 | 27664,99 | -3735 | 11,89% |
| 20 | 20990 | 19548,72 | -1441 | 6,87% |
| 21 | 16240 | 19729,58 | 3490 | 21,49% |
| 22 | 31790 | 29306,57 | -2483 | 7,81% |
| 23 | 26903 | 24947,07 | -1956 | 7,27% |
| 24 | 26719 | 29269,39 | 2550 | 9,55% |
| 25 | 19019 | 21443,2 | 2424 | 12,75% |
| 26 | 32289 | 27521,83 | -4767 | 14,76% |
| 27 | 17570 | 18276,61 | 707 | 4,02% |
| 28 | 26296 | 24152,68 | -2143 | 8,15% |
| 29 | 20580 | 17714,09 | -2866 | 13,93% |
| 30 | 30391 | 29606,94 | -784 | 2,58% |
| 31 | 22219 | 24499,65 | 2281 | 10,26% |
| 32 | 25074 | 29075,69 | 4002 | 15,96% |
| Среднее значение | 24601 | 24384,68 | -217 | 10,99% |
Таблица показывает, что наша модель дает достаточ?