Реферат: Начала термодинамики

Количество тепла, полученное каждой из фаз, можно представить в виде:

, (2.43)

Здесь введены обозначения – количество тепла, полученное от подсистемы I подсистемой II ( и наоборот), – количество тепла, полученное подсистемами из внешней среды.

Учитывая баланс теплоты:

,

см. 10 лист

(2.44)

или

(2.45)

Учитывая (2.9), запишем:

, (2.46)

Первая часть (2.46) характеризует теплообмен с внешней средой, а вторая создается за счет необратимого перехода тепла внутри системы. В соответствии с (2.10б) приращения энтропии всегда положительно. Прирост энтропии может быть равен нулю только после установления теплового равновесия:

Сделаем важное замечание о невозможности уменьшения энтропии в части закрытой системы при условии ее роста в системе в целом. То есть, ситуация, при которой

d_i S^I > 0 и d_i S^II < 0, d(S^I + S^II ) >0

физически нереализуема! Поэтому можно утверждать, что уменьшение энтропии в отдельной части системы, компенсируемое ее достаточным возрастанием в другой части системы является запрещенным процессом.

Отсюда следует, что в любом макроскопическом участке термодинамической системы приращение энтропии, обусловленное течением необратимых процессов, является положительным.

Такую формулировку второго начала термодинамики иногда называют “локальной” формулировкой. Ее основное значение состоит в том, что она позволяет провести более глубокий анализ необратимых процессов.

Обоснование “локальной” формулировки II-го начала возможно на основе методов статистической механики.

В дальнейшем анализе будет полезна производная от энтропии по времени:

(2.47)

Таким образом, направление потока тепла определяется знаком функции состояния (1/Т^I – 1/Т^II ).

Найдем прирост энтропии в открытых системах. Вначале пренебрежем химическими реакциями. Из уравнения (2.6) для открытых систем и второго начала термодинамики получим:

(2.48)

Применим это уравнение к закрытой системе, состоящей из двух открытых фаз I и II. Тогда для полного изменения энтропии системы можно записать:

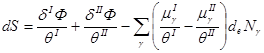(2.49)

Разделим суммарный поток энергии на следующие составляющие:

(2.50)

Здесь – количество тепла, получаемого от внешней среды, δ^I _i Ф и δ^II _i Ф – потоки энергии, поступающие от фазы II в фазу I и наоборот.

Тогда (2.49) принимает вид:

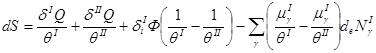(2.51)

Разделяя в (2.51) изменение энтропии dS на поток энтропии d_e S и прирост энтропии внутри системы d_i S и учитывая (2.9), запишем:

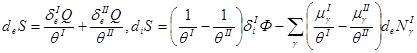(2.52).

Прирост энтропии d_i S обусловлен переносом тепла и вещества между двумя фазами системы (подсистемами).

Для приращения энтропии в единицу времени можно записать:

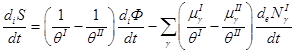≥0 (2.53)

Таким образом, скорость приращения энтропии представляет собой некоторую линейную функцию скоростей необратимых процессов.

Обобщим полученные результаты на непрерывные системы, в которых аддитивные параметры состояния являются не только функциями времени, но и непрерывными функциями пространственных координат. Такие системы иногда называют непрерывными системами.

Так, закон сохранения массы для непрерывной системы принимает вид:

(2.54)

Здесь – скорость движения …?. Если мы говорим о смеси, то:

(2.55)

где – макроскопические скорости движения отдельных компонент смеси.

Поток компонента γ смеси можно представить в виде суммы потока со средней массовой скоростью и “диффузионного” потока. Так,

(2.56)

Здесь ∆_γ – скорость диффузии по отношению к . Причем, .