Реферат: Надійність електронних апаратів
Рисунок 1 - Функціональна залежність P (t) та q (t)
Розглянемо більш докладно безвідмовність неремонтованих елементів. Показниками безвідмовності неремонтованих елементів є: ймовірність безвідмовної роботи P (t), частота відмов f (t), інтенсивність відмов λ (t) та середнє напрацювання до першої відмови Тср .
Під частотою відмов елементів (об’єктів) розуміють кількість відмов в одиницю часу, віднесену до початкової кількості поставлених на випробовування елементів. За статистичними даними частота відмов:
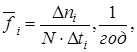 (3)
(3)
де Δni - кількість відмов за інтервал часу Δti ; N - кількість поставлених на випробування елементів; Δti - час випробовувань.
При цьому елементи, які відмовили у процесі випробовування, не замінюються новими і кількість працюючих елементів поступово зменшується.
Функцію частоти відмов можна записати у такому вигляді:
![]() (4)
(4)
При Δt →0 ймовірність відмови за час від 0 до t може бути визначена інтегруванням функції f (t) у цьому ж інтервалі:
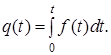
Тоді за час t ймовірність безвідмовної роботи:
 (5)
(5)
Щоб отримати залежність між P (t) та f (t) у більш наочному вигляді, слід продиференціювати попереднє рівняння (5). Отримуємо:
![]() або
або ![]() (6)
(6)
Таким чином, функція частоти відмов f (t) є похідна від функції ймовірності безвідмовної роботи P (t), яка береться зі зворотним знаком. Вона характеризує швидкість зменшення надійності у часі.
Оскільки ![]() то замінивши у рівнянні (6) - P′ (t) на q′ (t), отримаємо частоту відмов:
то замінивши у рівнянні (6) - P′ (t) на q′ (t), отримаємо частоту відмов:
![]() (7)
(7)
Але q (t) є інтегральний закон розподілу часу безвідмовної роботи t0 , похідна від якого являє собою щільність розподілу ймовірності випадкової величини t0 . Отже, функція частоти відмов f (t) - це щільність розподілу часу безвідмовної роботи, тобто диференціальний закон розподілу випадкової величини t0 .
Отримані формули (5), (6) та (7) визначають взаємодії P (t), q (t) і f (t).
Для системи, яка складається з ряду послідовно з’єднаних елементів, ймовірність безвідмовної роботи можна показати у вигляді добутку ймовірностей безвідмовної роботи всіх елементів:
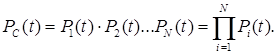 (8)
(8)
Критерієм, який найбільш повно характеризує надійність неремонтованих об’єктів, є інтенсивність відмов. На відміну від частоти відмов f (t), інтенсивність відмов характеризує надійність об’єкта у кожен даний момент, тобто його локальну надійність. Під інтенсивністю відмов слід розуміти кількість відмов в одиницю часу, віднесену до середньої кількості елементів, безвідмовно працюючих у даний проміжок часу. При цьому елементи, які відмовили, не замінюються новими.
З експериментальних даних ця характеристика знаходиться за формулою:
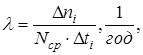 (9)
(9)
де Δni - кількість відмов за проміжок часу Δti ;
Ncp = (Ni =Ni+1 ) /2 - середня кількість працездатних елементів;
Ni - кількість елементів, працездатних на початку даного проміжку часу;
Ni+1 - кількість елементів, працездатних у кінці проміжку часу Δti .
Інтенсивність відмов λ (t) пов’язана однозначною залежністю з частотою відмов f (t) та ймовірністю безвідмовної роботи приладів P (t). Для того, щоб знайти цю залежність, змінимо формулу (9), розділивши чисельник і знаменник на N ·Δt , та, скориставшись співвідношеннями (1) і (3), отримаємо: