Реферат: Некоторые дополнительные вычислительные методы

и

, получим формулу Стирлинга

где .

Легко видеть, что при .

Кроме формулы Стирлинга, часто употребляется формула Бесселя. Для вывода этой формулы воспользуемся второй интерполяционной формулой Гаусса

.

Возьмем равностоящих узлов интерполирования с шагом , и пусть — заданные значения функции .

Если выбрать за начальные значения и , то, используя узлы , будем иметь:

.

Примем теперь за начальные значения и и используем узлы . Тогда , причем соответственно индексы всех разностей в правой части предыдущей формулы возрастут на единицу. Заменив в правой части этой формулы на и увеличив индексы всех разностей на 1, получим вспомогательную интерполяционную формулу:

.

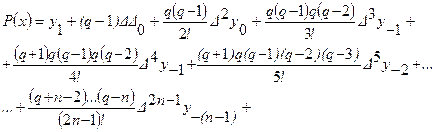
Взяв среднее арифметическое формул, после несложных преобразований получим интерполяционную формулу Бесселя

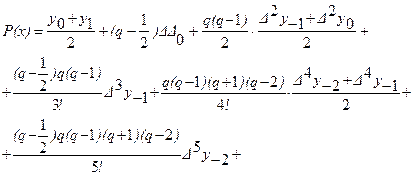
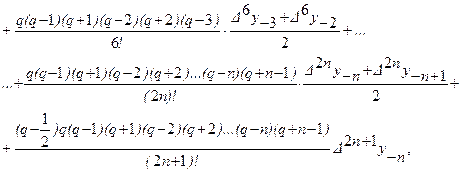
где .

Интерполяционная формула Бесселя, как следует из способа получения ее, представляет собой полином, совпадающий с данной функцией в точках .

Тригонометрическое интерполирование

Пусть функция f (х ) представлена на не­ко­то­ром отрезке [0, 2p]таблицей значений f (х_i ) в

рав­но­от­сто­ящих узлах х_i = 2p(i- 1)/ (2N+ 1), i = 1, 2, ...,2N+ 1. Тог­да три­го­но­мет­ри­чес­ким ин­тер­по­ли­ру­ю­щим мно­го­чле­ном на­зо­вем мно­го­член сте­­пе­ни m ви­­да:

.

Задача тригонометрической интерполяции со­с­­то­­ит в по­строении тригонометрического по­ли­но­ма, ко­то­рый бы на­­иболее полно удовлетворял ус­ло­­виям Р_m (х_i )= f (х_i ) для лю­­бого i= 1, 2, ..., 2 N+ 1.

Можно показать, что решением этой задачи яв­ля­­ет­ся полином именно того вида, коэффициенты ко­то­рого вы­чис­ля­­ют по сле­ду­ю­щим формулам:

;

;

.

Интерполяция сплайнами

Пусть отрезок [a, b] разбит на n равных частей [x_i , x_i+1 ], где x_i =a+ih, i=0, ..., n, x_n =b,

h=(b-a)/n.

Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a, b], а на каждом частичном отрезке [x_i , x_i+1 ] в отдельности является некоторым алгебраи­чес­ким многочленом.

Максимальная по всем частичным отрезкам степень многочленов называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной - дефектом сплайна.

На практике широкое распространение получили сплайны третьей степени, имеющие на [a, b] непрерывную, по крайней мере, первую производную. Эти сплайны называются кубическими и обозначаются S₃ (x).