Реферат: О неопределенных бинарных квадратичных формах

В алгебраической теории квадратичных форм (т.е. в теории квадратичных форм над полями) рассматриваются формы, у которых второй коэффициент без множителя , т.е.

.

Но в арифметической теории квадратичных форм (т.е. в теории форм над кольцами и в первую очередь над кольцом целых чисел) более предпочтительной является запись вида (1).

Определение 2. Бинарная квадратичная форма (1) называется классически целой (или целочисленной по Гауссу), если в ней коэффициенты являются целыми числами.

Мы будем в основном рассматривать только классические квадратичные формы и называть их просто численными.

Определение 3. Бинарные целочисленные квадратичные формы и называются собственно эквивалентными, если существует линейная подстановка переменных

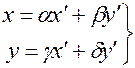(2)

с целыми коэффициентами и определителем , переводящая форму в форму , т.е. такая, что выполняется равенство

(3)

и несобственно эквивалентными, если целочисленная подстановка (2) с определителем переводит форму в форму . Эквивалентность таких форм обозначаем так: ~

Из (3) и (2) следуют соотношения

(4)

связывающие коэффициенты двух эквивалентных форм и .

Определение 4. Дискриминантом бинарной квадратичной формы называется число .

Предложение 1. Эквивалентные бинарные квадратичные формы имеют один и тот же дискриминант.

Доказательство. Пусть форма эквивалентна (собственно или несобственно) форме. Тогда по определению 3 существуют целые числа с определителем , при которых выполнены соотношения (4). Из них получаем

,

т.е. предложение 1 доказано.

Заметим, что обратное утверждение вообще говоря неверно, т.е. из того, что бинарные квадратичные формы имеют один и тот же дискриминант еще не следует, что они эквивалентны. Следующий общий факт приведем без доказательства.

Предложение 2. Отношение собственной эквивалентности бинарных квадратичных форм обладает свойствами рефлексивности, симметричности и транзитивности.

Определение 5. Если для квадратичной формы и для целого числа при некоторых целых и выполняется равенство , то говорят, что квадратичная форма представляет число .

Пример. Квадратичная форма представляет число , т.к. число является значением квадратичной формы при , т.е. равенство выполняется при .

Предложение 3. Эквивалентные бинарные квадратичные формы представляют одно и то же множество целых чисел.

Доказательство. Пусть формы и эквивалентны. Тогда существует унимодулярная целочисленная подстановка переменных:

и, значит,

.

Положив теперь в этом равенстве , получим

,

т.е. форма тоже представляет число . Поскольку отношение эквивалентности бинарных квадратичных форм обладает свойством симметричности (предложение 2) то и любое число, представимое формой будет представимое и формой .