Реферат: О неопределенных бинарных квадратичных формах
НОД ![]() . В остальных случаях форма называется не примитивной.
. В остальных случаях форма называется не примитивной.
Определение 10. Пусть ![]() - наибольший общий делитель чисел
- наибольший общий делитель чисел ![]() для формы
для формы ![]() определителя
определителя ![]() . Множество бинарных квадратичных форм с одними и теми же
. Множество бинарных квадратичных форм с одними и теми же ![]() и (при
и (при ![]() ) с одним и тем же знаком крайних коэффициентов
) с одним и тем же знаком крайних коэффициентов ![]() называется порядком форм.
называется порядком форм.
Так как ![]() и знаки получающихся коэффициентов
и знаки получающихся коэффициентов ![]() при
при ![]() не меняются при переходе от данной формы к эквивалентной ей форме, то порядок состоит из нескольких классов.
не меняются при переходе от данной формы к эквивалентной ей форме, то порядок состоит из нескольких классов.
При ![]() формы и порядок называются собственно примитивными, а при
формы и порядок называются собственно примитивными, а при ![]() и
и ![]() (
(![]() )- несобственно примитивными. Собственно и классы форм называются собственно примитивными и несобственно примитивными.
)- несобственно примитивными. Собственно и классы форм называются собственно примитивными и несобственно примитивными.
Возникает вопрос: конечно или бесконечно число целочисленных приведенных неопределенных форм. Ответ дает следующее.
Предложение 5. Число всех целочисленных приведенных неопределенных форм с заданным дискриминантом конечно.
Доказательство см. [2,п.185].
§2. О периодах неопределенных бинарных квадратичных уравнений
Теория неопределенных бинарных квадратичных форм существенно отличается от теории определенных форм наличием периодов приведенных форм. Гаусс первым обнаружил это явление и глубоко вник в природу приведенных форм с положительным неквадратным дискриминантом в связи с решением основных задач этой теории (см. [1,2]). В этом параграфе мы дадим основные свойства периодов неопределенных форм.
Нашему изложению мы сначала предпошлем те основные понятия из гауссовой теории квадратичных форм, которые нам понадобятся в дальнейшем (см. [1,2]).
Определение 1. формой соседней справа к целочисленной форме ![]() называется форма
называется форма ![]() , которая получается из формы
, которая получается из формы ![]() подстановкой
подстановкой 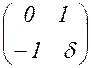 , где
, где ![]() -некоторое целое число.
-некоторое целое число.
Заметим, что при такой подстановке форма ![]() собственно эквивалентна форме
собственно эквивалентна форме ![]() . Зависимость между соседними формами
. Зависимость между соседними формами ![]() и
и ![]() можно охарактеризовать так: во-первых, формы
можно охарактеризовать так: во-первых, формы ![]() и
и ![]() имеют одинаковый дискриминант; во-вторых, последний коэффициент
имеют одинаковый дискриминант; во-вторых, последний коэффициент ![]() формы
формы ![]() является вместе с тем первым коэффициентом формы
является вместе с тем первым коэффициентом формы ![]() ; в третьих, сумма их средних коэффициентов
; в третьих, сумма их средних коэффициентов ![]() делится на
делится на ![]() .
.
Аналогичным образом определяется соседняя слева форма ![]() к форме
к форме ![]() .
.
Из определения соседних форм непосредственно следует
Предложение 1. Соседние формы собственно эквивалентны.
С помощью процесса нахождения последовательных соседних форм мы придем к другому важному понятию периода приведенных форм. Именно, пусть ![]() -приведенная форма дискриминанта
-приведенная форма дискриминанта ![]() и для нее
и для нее ![]() является соседней справа; для
является соседней справа; для ![]() форма
форма ![]() является соседней справа; для
является соседней справа; для ![]() форма
форма ![]() является соседней справа и т.д. Тогда все формы
является соседней справа и т.д. Тогда все формы ![]() ,
,![]() ,
,![]() ,…, являются собственно эквивалентными между собой, так и форме
,…, являются собственно эквивалентными между собой, так и форме ![]() .
.
Так как в силу предложения 5 §1 число всех целочисленных приведенных неопределенных бинарных квадратичных форм с заданным дискриминантом конечно, то в бесконечном ряду форм ![]() ,
,![]() ,
,![]() ,
,![]() ,… не все формы могут быть различными между собой. Если предположить, что
,… не все формы могут быть различными между собой. Если предположить, что ![]() и
и ![]() совпадают, то формы
совпадают, то формы ![]() и
и ![]() будут приведенными соседними слева для одной и той же приведенной формы и потому будут совпадать. Поэтому
будут приведенными соседними слева для одной и той же приведенной формы и потому будут совпадать. Поэтому ![]() и
и ![]() и т.д. будут совпадать. Следовательно, в ряду
и т.д. будут совпадать. Следовательно, в ряду ![]() ,
,![]() ,
,![]() ,… обязательно повторится первая форма
,… обязательно повторится первая форма ![]() и если
и если ![]() - первая форма в этом ряду, совпадающая с
- первая форма в этом ряду, совпадающая с ![]() , то все формы
, то все формы ![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() различны между собой.
различны между собой.
Определение 2. Совокупность различных последовательных соседних приведенных неопределенных форм ![]() ,
,![]() ,
,![]() ,…,
,…,![]() называется периодом формы
называется периодом формы ![]() .
.
Приведем несколько общих замечаний об этих периодах, следующих из их определения (см. [2]).
Предложение 2. Если формы ![]() ,
,![]() ,
,![]() ,… представлены следующим образом
,… представлены следующим образом
![]() ,
, ![]() ,
, ![]() ,…,
,…,![]() ,
, ![]() ,
, ![]() ,…, то все величины
,…, то все величины ![]() будут иметь одинаковые знаки, причем
будут иметь одинаковые знаки, причем ![]() все будут положительны.
все будут положительны.
Отсюда получается следующее свойство периодов.
Предложение 3. Количество квадратичных форм, из которых состоит период заданной формы ![]() всегда четно.
всегда четно.
Доказательство предложения 3 см. [1,2].
Заметим, что каждая форма ![]() , которая содержится в периоде формы
, которая содержится в периоде формы ![]() будет иметь тот же период, что и
будет иметь тот же период, что и ![]() .Именно, этот период будет таков:
.Именно, этот период будет таков:
![]() .
.
Отсюда получается следующее свойство периодов.
Предложение 4. Все целочисленные неопределенные бинарные квадратичные формы с одинаковым дискриминантом могут быть разбиты на периоды.
Доказательство (см. [2] разд. V, п.187) основано на том их свойстве, что периоды либо совпадают либо они попарно не пересекаются и каждая форма попадет только в один из периодов.
Пример. Все приведенные неопределенные формы с дискриминантом ![]() разбиваются на следующие шесть периодов:
разбиваются на следующие шесть периодов:
I. ![]() ;
;
II. ![]() ;
;
III. ![]() ;
;
IV.![]() ;
;
V. ![]() ;
;
VI. ![]() .
.
Видим что в каждом периоде содержится четное число приведенных форм: в периодах I и II по четыре формы, а в остальных периодах по шесть форм.