Реферат: О неопределенных бинарных квадратичных формах

О числе приведенных неопределенных бинарных квадратичных форм, так и о числе классов неопределенных квадратичных форм известно очень мало. Для числа классов бинарных квадратичных форм имеется точная формула Дирихле. Другим важным результатом являются неравенства, принадлежащие немецкому математику Зигелю.

,

где - число приведенных неопределенных бинарных квадратичных форм дискриминанта ; и - положительные постоянные, зависящие от ; причем - любое фиксированное положительное число. Наша цель состоит в том, чтобы элементарным способом доказать верхнюю оценку в неравенствах Зигеля для . Приводимое доказательство будет опираться на некоторые свойства функции числа положительных делителей натурального числа и мы их приведем вначале.

Арифметическая функция определяется как число положительных делителей натурального числа .

Предложение 1. Функция мультипликативна, т.е. , если .

Из этого предложения 1 легко выводится следующее

Предложение 2. Если 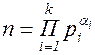- каноническое разложение натурального числа , то

.

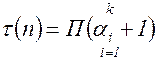Доказательства предложений 1 и 2 приводятся во всех учебниках по теории чисел (напр. см. [4,6]).

Предложение 3. Для числа делителя натурального числа имеет место неравенство

.

Доказательство. Пусть и - канонические разложения чисел и , и пусть

, ,…,- все простые делители наибольшего общего делителя чисел и . Тогда ясно, что

. (1)

Но так как справедливо неравенство

, (2)

то неравенство (1) с учетом (2) и предложения 2 перейдет в следующие соотношения

.

Предложение 3 доказано.

Предложение 4. Для имеет место неравенство

,

где - произвольное положительное число, - постоянная, зависящая только от .

Доказательство. Мы следуем рассуждениям в [4,5] (доказательство имеется также в [3]). Пусть - каноническое разложение числа . Тогда имеем

.

Рассмотрим отношение 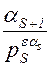, в случаях 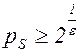и .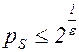

Если 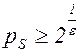, то 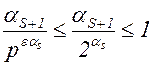, так как .

Если 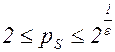, то считая , получим

.
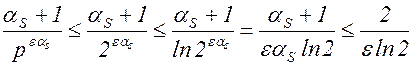