Реферат: О неопределенных бинарных квадратичных формах
Определение 3. Формы ![]() и
и ![]() , и их классы называются обратными: если
, и их классы называются обратными: если ![]() - один из этих классов, то другой класс
- один из этих классов, то другой класс ![]() будет обратным к классу
будет обратным к классу ![]() в смысле композиции классов.
в смысле композиции классов.
Замечание . Так как форма ![]() переводится в форму
переводится в форму ![]() подстановкой
подстановкой 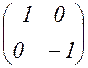 определителя
определителя ![]() , то каждая форма класса
, то каждая форма класса ![]() несобственно эквивалентна каждой форме из обратного класса
несобственно эквивалентна каждой форме из обратного класса ![]() и обратно, при несобственной эквивалентности двух форм их классы будут обратными. (при этом еще учитывается, что если форма
и обратно, при несобственной эквивалентности двух форм их классы будут обратными. (при этом еще учитывается, что если форма ![]() несобственно эквивалентна
несобственно эквивалентна ![]() , а
, а ![]() собственно эквивалентна
собственно эквивалентна ![]() , то
, то ![]() несобственно эквивалентна
несобственно эквивалентна ![]() ).
).
Определение 4. Класс бинарных квадратичных форм, совпадающий с обратным, называется двусторонним классом.
Из этого определения с учетом сделанного выше замечания получается
Предложение 5. Каждая форма двустороннего класса несобственно эквивалентна самой себе.
Доказательство. Пусть ![]() - двусторонний класс и
- двусторонний класс и ![]() . Покажем, что
. Покажем, что ![]() несобственно эквивалентна самой себе. Обозначим
несобственно эквивалентна самой себе. Обозначим ![]() .
.
Тогда форма ![]() и пусть
и пусть ![]() переводится в
переводится в ![]() подстановкой
подстановкой  и запишем это в следующем виде:
и запишем это в следующем виде: ![]() . Т.к.
. Т.к. ![]() - двусторонний класс, т.е.
- двусторонний класс, т.е. ![]() , то
, то ![]() . Но так как
. Но так как ![]() , то
, то ![]() и
и ![]() собственно эквивалентны, то найдется подстановка
собственно эквивалентны, то найдется подстановка ![]() определителя
определителя ![]() , что
, что ![]() . Тогда получаем
. Тогда получаем ![]() , т.е.
, т.е. ![]() . Но так как
. Но так как  , то форма
, то форма ![]() несобственно эквивалентна самой себе.
несобственно эквивалентна самой себе.
Предложение 5 доказано.
Определение 5. Форма ![]() , в которой
, в которой ![]() делится на
делится на ![]() , называется двусторонней.
, называется двусторонней.
Следующие два предложения дают некоторую информацию о строении двусторонних классов.
Предложение 6. В каждом двустороннем классе содержится по крайней мере одна двусторонняя форма.
Предложение 7. В каждом двустороннем классе положительного дискриминанта содержатся две и только две приведенные двусторонние формы.
Доказательство этих предложений имеются в [1,2].
Перейдем теперь к изложению основных результатов этого параграфа. Возникает еще вопрос: всегда ли двусторонняя форма принадлежит некоторому двустороннему классу. Ответ дает следующая теорема
Теорема 1. Каждая двусторонняя форма принадлежит некоторому двустороннему классу .
Доказательство. Пусть ![]() - двусторонняя форма, т.е.
- двусторонняя форма, т.е. ![]() (
(![]() делится на
делится на ![]() ) и обозначим ее класс через
) и обозначим ее класс через ![]() . Покажем, что
. Покажем, что ![]() -двусторонний класс. По определению обратная к
-двусторонний класс. По определению обратная к ![]() форме
форме ![]() . Так как
. Так как ![]() , то форма
, то форма ![]() переводится в себя подстановкой
переводится в себя подстановкой  . Далее имеем, что
. Далее имеем, что ![]() переводится в
переводится в ![]() подстановкой
подстановкой

определителя 1, т.е. ![]() и
и ![]() собственно эквивалентны. Тогда они принадлежат одному и тому же классу, т.е.
собственно эквивалентны. Тогда они принадлежат одному и тому же классу, т.е. ![]() и значит,
и значит, ![]() - двусторонний класс.
- двусторонний класс.
Теорема 1 доказана.
В связи с предложением 7 возникает еще следующий вопрос: могут ли быть в периоде форм двустороннего класса приведенные двусторонние формы соседними друг другу? Следующее утверждение дает необходимое условие того, что двусторонние приведенные формы будут соседними.
Теорема 2. Для того чтобы двусторонние примитивные приведенные формы ![]() и
и ![]() из двустороннего класса дискриминанта
из двустороннего класса дискриминанта ![]() были соседними необходимо, чтобы
были соседними необходимо, чтобы ![]() , где
, где ![]() - целая часть числа
- целая часть числа ![]() .
.
Доказательство. Пусть формы ![]() и
и ![]() соседние. Тогда
соседние. Тогда ![]() , где
, где ![]() - некоторое целое число. Так как
- некоторое целое число. Так как ![]() и
и ![]() - двусторонние формы, то
- двусторонние формы, то ![]() и
и ![]() , где последнюю делимость можно заменить следующим условием:
, где последнюю делимость можно заменить следующим условием: ![]() или что тоже самое
или что тоже самое  , откуда
, откуда ![]() . Тогда в силу взаимной простоты
. Тогда в силу взаимной простоты ![]() и
и ![]() (это следует из примитивности формы
(это следует из примитивности формы ![]() ) из условий делимости
) из условий делимости ![]() и
и ![]() следует, что
следует, что ![]() . Но так как
. Но так как ![]() , то
, то  или что тоже самое
или что тоже самое  . Из последнего условия делимости следует неравенство
. Из последнего условия делимости следует неравенство ![]() , откуда
, откуда ![]() . Но так как форма
. Но так как форма ![]() приведенная, то для числа
приведенная, то для числа ![]() должны выполняться неравенства
должны выполняться неравенства ![]() , из которых в свою очередь следует, что
, из которых в свою очередь следует, что ![]() .
.
Теорема 2 доказана.
Пример. Для ![]() следующие четыре периода по две соседние двусторонние формы
следующие четыре периода по две соседние двусторонние формы
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
При этом эти формы удовлетворяют теореме 2, т.к. ![]() .
.