Реферат: Обобщенный принцип наименьшего действия
Введены континуально многозначные функции, позволяющие адекватно описывать физические задачи. Показано их отличие от разрывных функций. Сформулирована и решена вариационная задача для функционалов с разрывным интегрантом, зависящих от линейных интегральных операторов, действующих на искомую оптимизируемую функцию, причем ядро оператора и оптимизируемая функция могут быть континуально непрерывными. С помощью таких операторов можно адекватно описывать распределенные частицы.
Хорошо известный в физике принцип наименьшего действия [1] основан на классическом вариационном исчислении, когда функционал зависит от экстремали и ее производных, применим только для нейтральных частиц. В заметке [2] показано, что для заряда ускорение запаздывает по отношению к возмущающей силе за счет лоренцевых сил трения, т.е. для заряда существует некоторая переходная импульсная характеристика, а движение заряда можно описать интегральным оператором. Поэтому для зарядов, когда нельзя связать значение ускорения в данный момент со значением возмущения в тот же (или другой) момент, принцип наименьшего действия неприменим. Для таких задач требуется другой математический аппарат. Обобщенный принцип наименьшего действия основан на методах обобщенного вариационного исчисления. Рассмотрим его.
1. Континуально многозначные функции
В последнее время негладкие, разрывные и сингулярные функции стали привлекать внимание [3-5]. Построен пример непрерывно дифференцируемой разрывной функции на пространстве D - бесконечно дифференцируемых финитных функций [4]. При решении вариационных задач экстремалями иногда оказываются негладкие, т.н. разрывные или сингулярные функции [3, 5]. Однако понятие разрывности функций в точках разрыва) не всегда соответствует физическим и математическим объектам - непрерывным кривым, которые они фактически описывают.
Рассмотрим кривую - прямоугольный импульс (рис. 1), определенный и непрерывный на всей оси абсцисс. Подобные объекты можно представить не только математически: например, так можно представить разложенную на плоской поверхности веревку. Но если про прямую b мы говорим, что она существует, и пишем ![]() при
при![]() , то про точки x=0 и x=1 говорится, что в них функция терпит разрыв первого рода, а прямых a и c как бы нет, хотя веревка физических разрывов не имеет.
, то про точки x=0 и x=1 говорится, что в них функция терпит разрыв первого рода, а прямых a и c как бы нет, хотя веревка физических разрывов не имеет.

Рис.1. Непрерывная кривая - прямоугольный импульс
По-видимому, объясняется это тем, что рассмотрения многозначных функций традиционно стараются избегать. В нашем же случае точкам x=0 и x=1 соответствуют замкнутые отрезки [0,1], параллельные оси ординат, т.е. одной точке на оси абсцисс соответствует множество точек на оси ординат, имеющее мощность континуума. Получается не просто многозначность, а многозначность мощности континуума.
Рассмотрим характерный пример - первую введенную в физике разрывную функцию - функцию Хевисайда, которая определяется [6-8] как предел последовательностей непрерывных функций, имеющих все производные. Поэтому график предельной функции вроде бы должен быть непрерывным. Этому противоречит определение функции Хевисайда, данное, например, в монографиях [6-8],
 (1.1)
(1.1)
Введем уточненное определение функции включения, соответствующее предельному переходу в эквивалентных последовательностях [6] непрерывных функций, имеющее непрерывный график,
 (1.2)
(1.2)
Если функцию включения (1.2) можно представить в виде непрерывной веревки, разложенной на плоской поверхности, то функция Хевисайда представляется той же веревкой, из которой вырезан кусок (сегмент [0,1]) в точке x=0. Обе функции имеют равные односторонние пределы, но разные графики при x=0 и вытекающие из этого свойства.
На первый взгляд, определение (1.2) непривычное, но фактически оно не новое. Когда говорят о значении определенного интеграла от положительной подынтегральной функции, то имеют в виду, что он "равен площади криволинейной трапеции, ограниченной графиком подынтегральной функции, осью абсцисс и прямыми, параллельными оси ординат, построенными на концах отрезка интегрирования" [8].
Поскольку определенный интеграл в конечных пределах от a до b всегда можно выразить с помощью сдвинутых функций включения H(x) через интеграл с бесконечными пределами
 (1.3)
(1.3)
то функции включения (1.2) как раз и описывают "прямые, параллельные оси ординат", чего не скажешь о функции Хевисайда (1.1).
Замечание. Из формулы (1.3) следует, что все интегрируемые функции фактически определены на всей оси абсцисс, что позволяет, обладая методикой решения разрывных экстремальных задач, например, приведенной в монографии [5], легко решать их, когда экстремум не внутренний, а достигается на границе замкнутого отрезка [a,b].
Используя определение функции включения (1.2), функцию, изображенную на рис.1, - прямоугольный импульс - можно записать:

Предложенное непротиворечивое определение непрерывной функции включения позволяет адекватно описывать непрерывные кривые в точках математической разрывности. Сам термин "разрывная функция" выбран несколько неудачно. Фактически мы имеем дело с непрерывными функциями, обладающими многозначностью мощности континуума. Действительно разрывными являются функции типа функции Хевисайда (1.1), но фактически, когда говорится о "разрывных функциях", в большинстве случаев имеются в виду функции вида (1.2).
Интересно отметить, что популярные пакеты компьютерных программ для решения прикладных задач и построения графиков EUREKA и MATHEMATICS дают графическое изображение функции включения, записанной как H(x)=(1+sgn(x))/2, именно в виде формулы (1.2). В монографии [5] в графиках также используется непрерывная функция включения (1.2), хотя это определение и не приводится.
Наглядное представление d -функции в виде обычной функции в математической литературе отрицается, поэтому при решении экстремальных негладких и разрывных задач понятие d -функции не используется [3, 5]. Для аналитического решения экстремальных задач требуется уточнение определения в d -функции.
Для уточнения определения введенной Дираком сингулярной функции - d -функции введем d -образную эквивалентную последовательность [6, 9] через функции включения (1.2)
 (1.4)
(1.4)
При любом значении a существует интеграл
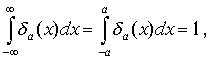
и предел формулы (1.4) при a- 0 является d -функцией, т.е.
![]() (1.5)
(1.5)
Так определенная (1.4)-(1.5) d -функция является пределом непрерывного графика прямоугольного импульса высотой 1/2a и шириной 2a. При a- 0 высота "стенок" прямоугольного импульса неограниченно возрастает, а ширина импульса стремится к 0. В пределе "стенки" "слипаются" в один луч - d -функцию, расположенную в начале координат.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--