Реферат: Образцы исследования элементарных функций, содержащих обратные тригонометрические функции
Имеем:
![]()
Откуда
![]()
2. Аналогично
![]() , где 0 < x < 1, 0 < y < 1
, где 0 < x < 1, 0 < y < 1
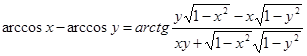 , где 0 < x < 1, 0 < y < 1
, где 0 < x < 1, 0 < y < 1
![]()
![]()
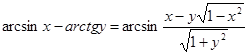
Формулы сложения аркфункций от произвольных аргументов.
1. Выразить сумму ![]() через арксинус
через арксинус
По определению арксинуса
![]() и
и ![]() ,
,
откуда
![]()
Для дуги γ возможны следующие три случая:
Случай 1: ![]()
Если числа x и y разных знаков или хотя бы одно из них равно нулю, то имеет место случай 1.
В самом деле, при ![]() и
и ![]() , имеем:
, имеем:
![]() , и
, и ![]() ,
,
откуда
![]()
При x > 0, y > 0 для дуги γ имеет место одна из следующих двух систем неравенств:
а) ![]() б)
б) ![]()
Необходимым и достаточным признаком, позволяющим отличить один от другого случаи а) и б), является выполнение неравенства:
![]() в случае а) и
в случае а) и ![]() в случае б)
в случае б)
В самом деле, взаимно исключающие друг друга соотношения а) и б) влекут за собой взаимно исключающие следствия ![]() и
и ![]() (соответственно), а потому эти следствия служат необходимыми и достаточными признаками наличия данных соотношений.
(соответственно), а потому эти следствия служат необходимыми и достаточными признаками наличия данных соотношений.
Вычислив ![]() , получим:
, получим:
![]()