Реферат: Операторы в вейвлетном базисе
![]() , (1.2)
, (1.2)
и представим пространство L2 ( R d ) в виде прямой суммы
![]() (1.3)
(1.3)
Выбирая масштаб n , можем заменить последовательность (1.1) следующей последовательностью:
![]() (1.4)
(1.4)
и получить
![]() (1.5)
(1.5)
Если имеем конечное число масштабов, то, не нарушая общности, можно положить j=0 и рассматривать
![]() , V0 Î L2 ( R d ) (1.6)
, V0 Î L2 ( R d ) (1.6)
вместо (1.4). В числовой реализации подпространство V0 конечномерно.
Функция j - так называемая масштабирующая (скейлинг-) функция. С ее помощью можно определить функциюy - вейвлет - такую, что набор { y( x- k)} k Î Z образует ортонормальный базис в W0 . Тогда
![]() , m=0.. M-1 . (1.7)
, m=0.. M-1 . (1.7)
Из свойства 4’ непосредственно следует, что, во-первых, функция j может быть представлена в виде линейной комбинации базисных функций пространства V-1 . Так как функции { j j, k ( x)=2- j/2 j(2- j x- k)} k Î Z образуют ортонормальный базис в Vj , то имеем
![]() . (1.8)
. (1.8)
Вообще говоря, сумма в выражении (1.8) не обязана быть конечной. Можно переписать (1.8) в виде
![]() , (1.9)
, (1.9)
где
![]() , (1.10)
, (1.10)
а 2p-периодическая функция m0 определяется следующим образом:
![]() . (1.11)
. (1.11)
Во-вторых, ортогональность { j( x- k)} k Î Z подразумевает, что
![]() (1.12)
(1.12)
и значит
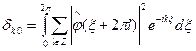 (1.13)
(1.13)
и ![]() . (1.14)
. (1.14)
Используя (1.9), получаем
![]() (1.15)
(1.15)
и, рассматривая сумму в (1.15) по четным и нечетным индексам, имеем
![]() . (1.16)
. (1.16)