Реферат: Оптимизационные модели межотраслевого баланса

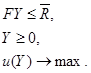(31)

где F = f (Е – А) ^{– 1} – матрица коэффициентов полных затрат ресурсов, .

Оптимальное решение этой модели всегда существует и является единственным. Оптимальный план Y * есть точка касания наибо­лее удаленной от начала координат поверхности безразличия и вы­пуклого многогранника, образованного условиями . Если эта поверхность безразличия касается вершины многогранника, то это означает полное использование нескольких ресурсов. Очевидно, что в случае применения ЦФП вероятность того, что точкой опти­мума будет вершина многогранника, выше, чем в случае приме­нения ассортиментного критерия. Однако вполне возможно, что максимум u (Y ) достигается на одной из граней многогранника, т. е. при полном использовании только одного ресурса.

Таким образом, общим свойством рассмотренных в этом пара­графе моделей является то, что оптимальный план чаще всего достигается при полном использовании только одного ресурса. А это означает, что только один вид ресурсов влияет на формирование оптимального решения. Данное свойство не адекватно экономиче­ской реальности; оно обусловлено недостатком моделей.

В моделях (24) , (27) , (30) почти отсутствуют возможности маневрирования ресурсами, имеющими различную дефицитность. По каждому виду продукции задается только один производствен­ный способ, а поэтому технология производства не реагирует на выявляющиеся в процессе оптимизации соотношения наличия ре­сурсов и потребностей в них. Благодаря корректировке исходных данных на основе анализа оптимальных решений этот недостаток можно преодолевать лишь отчасти.

Напрашивается вывод о том, что оптимизационные модели на­родного хозяйства должны включать условия выбора между раз­личными способами- производства одноименной продукции.

§3. ОПТИМИЗАЦИОННЫЕ МЕЖОТРАСЛЕВЫЕ МОДЕЛИ С ПРОИЗВОДСТВЕННЫМИ СПОСОБАМИ

Первый вариант модели (минимизация затрат труда на производство заданной конечной продукции).

Построим модель, представляющую собой непосредственное обобщение модели межотраслевого баланса, записанной в форме (22) . В модели предусматривается возможность выбора между различными производственными способами. Пусть каждый вид продукции производится несколькими способами , где T_j = {1, ... , s_j }. При этом каждым способом выпускается только один продукт. Введем новые обозначения:

– объем производства продукции j способом _j ;

– коэффициент пря­мых затрат продукции i на производство единицы продукции j способом _j ;

– затраты труда на единицу продукции j , произ­водимой способом _j .

Модель имеет вид:

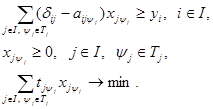(32)

Модель (32) всегда имеет решение, если выполняются усло­вия, аналогичные условию продуктивности матрицы коэффициен­тов прямых материальных затрат модели межотраслевого баланса. Например, одно допустимое решение может быть получено, если включить в план по одному способу для каждого вида продукции, а все остальные переменные считать равными нулю. Так может быть составлено систем уравнений межотраслевого баланса производства и распределения продукции, каждая из которых имеет решение, если матрица продуктивна.

Анализ модели позволяет выявить ряд ее интересных специфи­ческих свойств.

Теорема 1 . При положительном векторе конечной про­дукции Y ⁰ > 0 производятся все продукты и каждый продукт про­изводится только одним способом.

Доказательство. Напомним, что мы исходим из пред­положения, что оптимальный план – единственный. Введем в ус­ловия дополнительные переменные Δy_i (излишки конечной про­дукции сверх минимально необходимых объемов ), превращающие неравенства в равенства.

В каждом i -м уравнении

положительными являются только коэффициенты при переменных Х. Но поскольку все , то и все , т. е. оптимальном плане должны производиться все виды продуктов.

Максимальное число положительных переменных в оптимальном плане равно п (числу уравнений). Следовательно, в каждой сумме переменных положительной может быть только одна переменная. Иначе говоря, в оптимальном плане каждый продукт про­изводится только одним способом.

Следствие. Из теоремы следует, что поскольку число воз­можных положительных переменных исчерпывается переменными способов производства, то все Δy_i в оптимальном плане равны нулю. Иными словами, оптимальный план обращает исходные неравен­ства строго в равенства.

Введем дополнительные обозначения: X * – оптимальный план модели (каждая его компонента есть интенсивность применения какого-то «лучшего» способа производства); A * – матрица коэффи­циентов материальных затрат, составленная из способов, которые вошли в оптимальный план.

Матрица А* аналогична матрице А межотраслевого баланса с той лишь разницей, что вместо средневзвешенных коэффициентов из разных способов в ней представлены коэффициенты только «луч­ших» способов. Матрицы A * и (Е – А* ) обладают теми же экономико-математическими свойствами, что и матрицы межотраслевого ба­ланса. Среди этих свойств отметим, в частности, существование матрицы (Е – А* )^–1 ≥ 0. Элементы матрицы (Е – А* )^–1 являются коэффициентами полных потребностей в выпуске продукции для получения единицы конечной продукции в оптимальном плане. Оптимальный план удовлетворяет следующей системе уравнений:

(E – A ) X * = Y ⁰ или X * = (E – A )^–1 Y ⁰ .

Теорема 2. Базис оптимального плана, а следовательно, и выбор «лучших» способов остаются постоянными при любых из­менениях положительного вектора Y ⁰ .

Доказательство. Для того чтобы базис оптимального плана оставался неизменным при переменном векторе Y ⁰ , доста­точно – в соответствии с (15) ,– чтобы выполнялось условие

(E – A * )^–1 Y ⁰ ≥ 0.