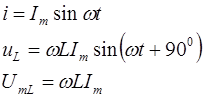Реферат: Основные понятия и элементы линейных пассивных электрических цепей
Вторым законом Кирхгофа можно пользоваться для определения напряжения между двумя произвольными точками схемы. В этом случае необходимо ввести в левую часть уравнений исходное напряжение вдоль пути, как бы дополняющего незамкнутый контур до замкнутого. Например, для определения напряжения Umn можно написать уравнение для контура mncb или nmbc:
Umn + I4 R4 + I3 R3 = E1 или - I3 R3 – Umn – I4 R4 = - E1
откуда легко можно найти искомое напряжение (необходимо при рассмотрении метода узловых потенциалов)
Анализ линейных электрических цепей при гармонических воздействиях.
Гармоническое возмущение – ток, напряжение или ЭДС, меняющиеся по гармоническому закону, записываются:
i(t) = Im sin( ω t + Ψi );
u(t) = Um sin( ω t + Ψu );
e(t) = Em sin( ω t + Ψe ).
Im, Um, Em – амплитуды;
( ω t + Ψ) – фазы;
Ψ – начальные фазы этих величин.
Их действующие значения равны: 
Амперметры и вольтметры, предназначенные для измерения тока, напряжения и ЭДС, меняющихся по гармоническому закону, градуированы в действующих значениях измеряемых величин.
Мы будем изучать методы анализа установившихся режимов линейных электрических цепей, составленных активными сопротивлениями, индуктивностями и ёмкостями при гармонических воздействиях. Сложность расчёта таких цепей обусловлена тем обстоятельством, что напряжения на индуктивностях и ёмкостях сдвинуты по фазе относительно токов через них протекающих.
Прежде всего, рассмотрим основные соотношения в линейных пассивных элементах цепи при гармоническом воздействии.
Активное сопротивление.
u = Um sin ω t
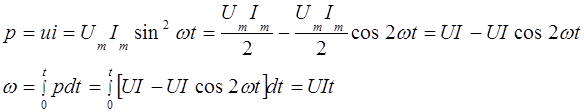
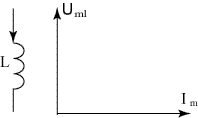
Индуктивный элемент.
i = Im sin ω t
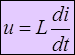
Емкостной элемент.
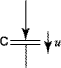u = Um sin ω t
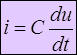
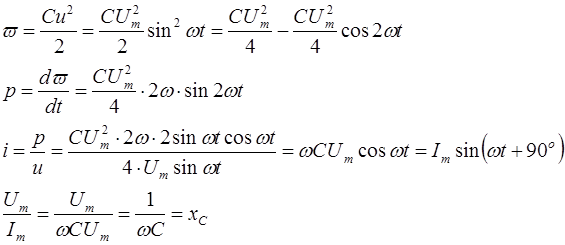
Анализ последовательной цепи переменного тока
Мы показали, что при заданном токе напряжения пассивных элементов будут следующими:
