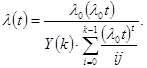Реферат: Основы теории надежности
Копер. (t, t) = Кг (t) · Р(t)
Для определения Копер. имеется статистическая оценка:
Законы распределения случайных величин, используемые в теории надежности.
Время m/q между соседними отказами для элементов аппарата является непрерывной случайной, величиной, которая характеризует некоторый закон распределения. Наиболее часто используется следующий закон распределения:
Экспонентой распределения Вейбула - называется нормальное распределение Y и другие распределения. Экспоненциальное OCH – показатель надежности при нем могут быть оценены исходя из следующей зависимости
Экспоненциальные показатели - основные показатели надежности при не при них могут оценены исходя из следующей зависимости: P(t) = e- l t ; Q(t) = 1 - e- l t ; или
l - это параметр экспоненциального распределения.
lt << 1, то Q(t) » lt = 1/Т; P(t) » 1 -lt = 1 –t /T.
Важным свойством экспоненциального распределения является вероятность безотказной работы в интервале t, t +t не зависящем от времени предшествующей работы t, а зависящей от длины интервала t.
Интервалы времени: (0, t); (0; t + t) значит P(t + t) = P(t) · P(t); - вероятность работы системы за время t при условии, что система безотказно проработала за время t.
Для экспоненциального закона ® P(t + t) = e- l (t + t ) ; P(t) = e- l t ; P(t) = e- l t .
В интервале времени (t + t) вероятность безотказной работы не зависит от времени работы t, а зависит от t.
Пример.
l = 0,01 (1/час); t = 50 (час).
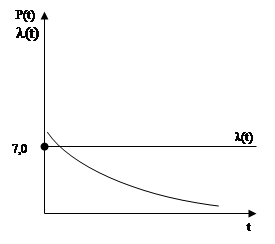Значит: Р(50) = е-0б01 · 50 = е-0,05 = 0,0607 Т = 1/l = 100 (час).
Распределение Рема:
d-параметр распределения Рема.
 |
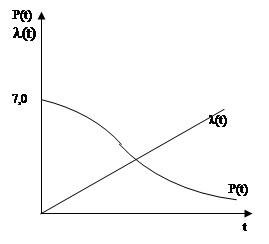Пример: d = 100r, t = 50r.
P(50) = 
Нормальное распределение:
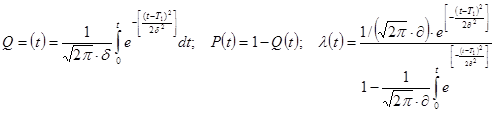
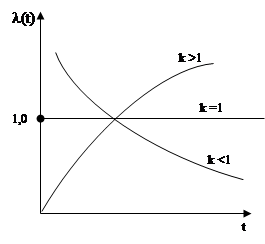
Y – распределение:
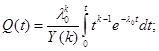
