Реферат: Основы теории надежности
Для сложной структуры анализ надежности системы сводится к представлению системы в виде некоторого элемента.
Графовероятностный метод. Основывается на представлении схемы расчета надежности в виде связного двухполюсного графа, имеющего два полюса: входной и выходной. Физически это можно представить как определение возможности прохождение некоторого сигнала от входа некоторой системы характерной сетевой структуры, к выходу.
Схемы распределения надежности различают по критерию работоспособности или отказа. Всевозможные структуры систем можно свести к последовательным и комбинированным.
Последовательные системы называются системы, которые работоспособны тогда, когда работоспособны все ее элементы. Если говорить о состоянии отказа, то последовательные системы отказывают, если отказывает хотя бы один ее элемент.

![]() Обозначим:
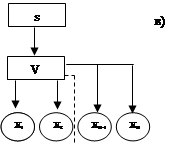
Обозначим: ![]() n – число элементов в последовательной системе, а событие состояний в работоспособной 8 – го элемента через х8 , а событие состояний b работоспособность всей системы через s, тогда схема расчета надежности по критерию работоспособности и отказа и по дереву работоспособности и отказа будут иметь следующий вид: в дереве работоспособности базисное событие, определяемое работоспособность элементов х8 , связано между собой логическими звеньями, а в дереве отказов базисное событие, определяемое, отказами элементов х8 связано между собой логическими звеньями или (v) ® схема расчета по критерию работоспособности изображена ниже:
n – число элементов в последовательной системе, а событие состояний в работоспособной 8 – го элемента через х8 , а событие состояний b работоспособность всей системы через s, тогда схема расчета надежности по критерию работоспособности и отказа и по дереву работоспособности и отказа будут иметь следующий вид: в дереве работоспособности базисное событие, определяемое работоспособность элементов х8 , связано между собой логическими звеньями, а в дереве отказов базисное событие, определяемое, отказами элементов х8 связано между собой логическими звеньями или (v) ® схема расчета по критерию работоспособности изображена ниже:
![]()
![]()
Схема распределения по критерию отказа. Схема расчета по дереву работоспособности.
 |
![]()
Схема расчета по дереву отказа.
 На рисунках соединены исходный узел А узлом Е расчеты, на схеме расчет надежности существует тогда, когда работоспособны все ее элементы. Из рисунка б) видно, что система отказывает, если хотя бы 1 элемент, поэтому начальные и конечные сигналы всех веток должны совпадать с начальным узлом системы А и конечным Е. Все события на рисунках представляют схему со включенными элементами.
На рисунках соединены исходный узел А узлом Е расчеты, на схеме расчет надежности существует тогда, когда работоспособны все ее элементы. Из рисунка б) видно, что система отказывает, если хотя бы 1 элемент, поэтому начальные и конечные сигналы всех веток должны совпадать с начальным узлом системы А и конечным Е. Все события на рисунках представляют схему со включенными элементами.
Надежность последовательной системной оценки определяется формулой: ![]()
Где Pi (t) коэффициент надежности. I – его элементная система.
Параллельные системы.
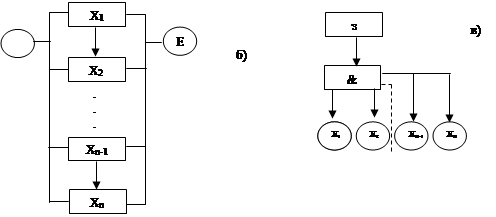
Называется такая система, которая работоспособна, если работоспособен хотя бы 1 из ее элементов, т.е. система отказывает тогда, когда отказывают все элементы. События состоят в том, что восьмой элемент работоспособен обозначим его как х8 где х8 = 1, 2…, n, n – число в системе. События состояния отказа s, тогда схема работоспособна и расчет по критерию работоспособности и отказа будет иметь следующий вид:
Схема расчета по критерию работоспособности.
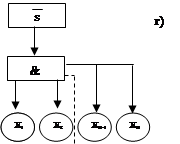
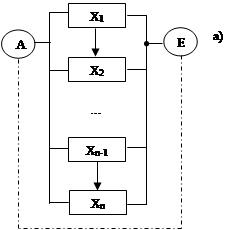 Схема расчета по критерию отказа.
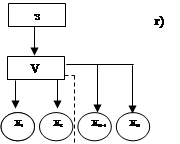
Схема расчета по критерию отказа.
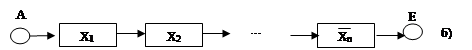 |
Схема расчета по дереву работы.
 |
Отказ.
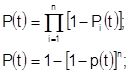
где Pi (t) –надежность i- того элемента.
Вторая формула пригодна для равно наделенных элементов.
Надежность системы с последовательно параллельной структурой.
Для последовательно параллельной структуры эффективным является метод свертки. Он основан на поэтапном преобразовании этой структуры в последовательные структуры.
 |
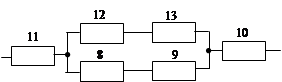 |
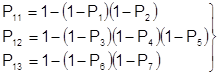 ;
; 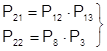 ;
;
Метод свертки.
Схема мажоритарного регулирования
 |
![]()
![]() P31 = 1 –(1 – P2 )(1 – P22 ) ==>
P31 = 1 –(1 – P2 )(1 – P22 ) ==>
P = (P11 · P31 · P10 )

 На выходе получается тот же сигнал большинство которых Р0 . Если РР0 =1 то: получим две схемы.
На выходе получается тот же сигнал большинство которых Р0 . Если РР0 =1 то: получим две схемы.
![]()
Не все схемы надежности можно представить в виде комбинации последовательной и параллельной. Поэтому для расчета схем используют приближенные методы.

Метод минимальных путей и сечений.
Минимальным путем называется такой j - минимальный путь, который состоит из min совокупности m подсистем, необходимый для безотказной работы системы независимо от состояния остальных подсистем.
В структуре системы есть несколько min путей. Характерным признаком min пути является то, что отказ хотя бы одной подсистемы (если работоспособна только подсистема одного пути) влечет за собой отказ системы.
Минимальное сечение это такое сечение k – min сечения, которое состоит из минимальной совокупности подсистемы Nk , чей одновременный отказ влечет за собой отказ системы независимо от состояния остальных подсистем.
Характерный сбой min сечения является то, что восстановлен хотя бы первая подсистема в min сечении (если остальные подсистемы работают) влечет за собой восстановление подсистемы.
Min сечения: 513, 524, 5164.