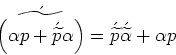Реферат: Полуточка модель скорости

(20)

Оставив члены первого порядка малости по :

(21)

Используя определение полуточки

получим:

(22)

Положив точку функцией величины и сравнив с разложением её в ряд Тейлора в окрестности , получим:

(23)

Это выражение и является определением скорости точки , если она движется во времени , испытывая в каждый его момент преобразование Пуанкаре:

(24)

Выражение (23) является скалярно-векторно сопряжённым самому себе:

(25)

То есть абсолютное приращение точки выполняется несмотря на произвольность величины так, что точка остается сама себе скалярно-векторно сопряжённой.

Отметим также, что в силу свойства точки верно равенство:

(26)

Далее...

Придерживаясь модели полной группы Пуанкере, мы должны считать величины и дуальными бикватернионами, имеющими 16 компонент. В силу требования скалярно-векторной сопряжённости самой себе точка часть компонентов имеет нулевыми.

Для понимания дальнейшего вывода представим величины и в виде, явно содержащем разделение на главную и дуальную части:

	(27)