Реферат: Полуточка модель скорости

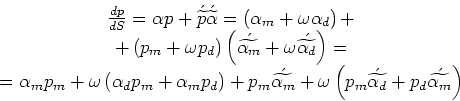
Сгруппировав главные и дуальные части, получим:

(28)

Используя это разложение в главных и дуальных частях и задавая различные частные случаи величин , , и , оценим характер вклада в скорость точки отдельных величин и . А также найдём их сопоставление отдельным общеизвестным скоростям.

Случай 1.

Зададим точку как дуальный вектор с единичной главной частью:

(29)

а величину как дуальный вектор с нулевой главной частью:

(30)

Тогда, используя разложение (29), найдем скорость точки при таком преобразовании:

(31)

В силу того, что выбрано условие , имеем:

(32)

Таким образом, в приведённых выше условиях величина является линейной скоростью приращения дуальной части . В силу того, что в состав величины входит как полярная, так и дуальная части, то есть:

(33)

то в силу свойств функций и , определённых как

	(34)
	(35)

И имеющих свойства сопрягаться:

	(36)
« 1 2 3 4 5 » К-во Просмотров: 726 Бесплатно скачать Реферат: Полуточка модель скорости >>> Скачать <<< Меню Поиск