Реферат: Построение математических моделей при решении задач оптимизации

Эта линейная функция будет иметь минимальное значение при х = 0, у min = 6000 т/км. Завод надо строить возле шахты А.

Для лучшего понимания этой задачи целесообразно дополнительно выяснить вопрос, где нужно бы построить завод, если бы:

а) в шахте А добывалось 100 т, а в шахте В – 200 т руды;

б) в шахте А – 200 т, а в шахте В – 190 т;

в) в шахте А и шахте В – по 200 т руды;

Чтобы решить этот вопрос, нужно найти на сегменте [0; 60] минимум функции:

а) у = 100х + 200(60 – х) = - 100х + 12000;

б) у = 200х + 190(60 – х) = 10х + 11400;

в) у = 200х + 200(60 – х) = 12000.

Из всего этого можно сделать такой вывод: если в шахте А добывается руды больше, чем в шахте В, то завод надо строить возле шахты А; если же количество руды в этих шахтах одинаковое, то завод можно строить в любом месте вблизи шоссейной дороги между шахтами А и В.

Задача 2.

На колхозной ферме нужно провести водопровод длиной 167 м. Имеются трубы длиной 5 м и 7 м. Сколько нужно использовать тех и других труб, чтобы сделать наименьшее количество соединений (трубы не резать)?

Учитывая, что количество как одних, так и других труб может изменяться, количество 7 – метровых труб обозначим через х , а 5 – метровых – через у. Тогда 7х – длина 7-метровых труб, 5у – длина 5-метровых труб. Отсюда получаем неопределенное уравнение

7х + 5у = 167

Выразив, например, переменную у через переменную х , получим:

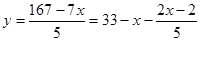
Так как х, уЄ Z, то методом перебора легко найти соответствующие пары значений х и у , которые удовлетворяют уравнение 7х + 5у = 167.

(1; 32), (6; 25), (11; 18), (16; 11), (21; 4).

Из этих решений наиболее выгодное последнее, т.е. х = 21, у = 4.

Задача 3 .

Для изготовления двух видов изделий Аи В завод расходует в качестве сырья сталь и цветные металлы, запас которых ограничен. На изготовление указанных изделий заняты токарные и фрезерные станки в количестве, указанном в таблице.

Таблица

Затраты на одно изделие		А	В	Ресурсы
Материалы	Сталь (кг)	10	70	320
Материалы	Цветные металлы (кг)	20	50	420
Оборудование	Токарные станки (станко-ч)	300	400	6200
Оборудование	Фрезерные станки (станко-ч)	200	100	3400
Прибыль на одно изделие (в тыс.руб.)		3	8

Необходимо определить план выпуска продукции, при котором будет достигнута максимальная прибыль, если время работы фрезерных станков используется полностью.

Решение.

Посмотрим математическую модель задачи. Обозначим через х число изделий вида А, а через у – число изделий вида В. На изготовление всей продукции уйдет (10 х +70у)кг стали и (20 х +50у) кг цветных металлов. Так как запасы стали не превышают 320 кг, а цветных металлов – 420 кг, то

10х +70у £ 320

20х + 50у £ 420

(300х +400у) ч – время обработки всех изделий на токарных станках:

300х + 400 £ 6200

Учитывая, что фрезерные станки используются максимально, имеем:

200х +100у = 3400