Реферат: Построение математических моделей при решении задач оптимизации

Ответ.Размеры окна 6/(p +4),12/(p +4).

Задача 6.

На учебном полигоне произведен выстрел из зенитного орудия в вертикальном направлении не разрывающимся снарядом. Требуется определить наибольшую высоту подъема снаряда, если начальная скорость снаряда ν₀ = 300 м/с. Сопротивлением воздуха пренебречь.

Решение.

Из курса физики известно, что путь s, пройденный телом при равноускоренномдвижении, изменяется в зависимости от времени по закону s = s₀ + ν₀ t + at² / 2, где s₀ – начальный путь, ν₀ – начальная скорость, a – ускорение, t – время.

В рассматриваемом случае s =0,v =300 м/с, а=-5 м/с ,значит,S(t) = 300t – 5t² .

??????? S(t) ????????? ?????????? ???????? ???

S(30)= 300*30-5*30² =4500(м)

Наибольшая высота подъема снаряда равна 4500 м.

Как видно из примеров, решение экстремальных задач дает возможность установить более тесную межпредметную связь алгебры, геометрии и физики. При их решении можно приобрести не только математическую информацию, но и знания из курса физики.

Решение физических задач поучительно с точки зрения математики, так как можно показать тонкости тех или иных математических приемов в действии, в их практическом приложении.

В частности, эти задачи помогают осознать, что функция, заданная аналитической формулой, может выражать зависимости между реальными величинами в самых различных явлениях и процессах

Задача 7.

Арка моста имеет форму параболы (высота 4 м, наибольшая ширина 20 м).

Составьте уравнение этой параболы.

Решение.

Уравнение параболы в данном случае имеет вид y = ax² + c. Для определения a и c подставим в этом уравнение координаты точек B и C (рис. 1), т.е.

4 = cc = 4 c = 4,

ÞÞ

0 = 100a + c 100a = -4 a = - 0,04

Парабола имеет вид: y = - 0,04x² + 4.

4.Применение методов дифференциального исчисления при решении прикладных задач.

Задача 8.

Проектируется канал оросительной системы с прямоугольным сечением в 4,5 м² . Каковы должны быть размеры сечения, чтобы для облицовки стенок и дна пошло наименьшее количество материала?

Решение.

Пусть стенки канала имеют длину x м., а дно канала – y м.

Тогда:

x*y=4,5 y=4,5/x

S= L*(2x+y) S=L*(2x+4,5/x)

Найдем производную.

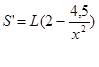Так как S’=0, и L(длина канала)-положительное число,то

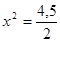x=1,5 Легко убедиться, что при данном x значение S минимально

Ответ: x=1,5 м. y=3 м.

Задача 9.