Реферат: Построение полуполевых плоскостей

1) Х≠ 1;

2) , Х≠ Y : ;

3) G= .

Рассмотрим аффинную плоскость, построенную следующим образом:

· точки плоскости – элементы группы G ,

· прямые – смежные классы группы G по подгруппам из множества S ,

· отношение инцидентности – естественное.

Достроим аффинную плоскость до проективной, назвав особыми точками множества смежных классов по одной и той же подгруппе, особой прямой – множество всех особых точек.

В качестве группы G может быть выбрано векторное пространство.

Пусть F – конечное поле, F= GF (q ). Рассмотрим n -мерное пространство W над полем F и 2 n -мерное пространство V= WW . Построим проективную плоскость на основе пространства V :

· аффинные точки – векторы , где , т.е. , ,

· аффинные прямые – смежные классы по подгруппам и , где ,

· особые точки и особые прямые вводятся, как описано выше.

Здесь – множество матриц размерности n n над полем F , причем:

1) R содержит и ;

2) все матрицы R , кроме нулевой – невырожденные, кроме того, .

Множество называют регулярным множеством плоскости (спрэдом).

Полуполевые плоскости порядка 16 построим на основе векторного пространства V размерности 4 над полем из 4 элементов, т.е. аффинные точки – это вектора вида , где , аффинные прямые – смежные классы по подгруппам:

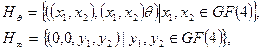
здесь .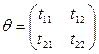

Напомним, что регулярное множество R замкнуто по сложению. Тогда праведлива следующая лемма:

Лемма 2.1. Плоскость трансляций координатизируется полуполем тогда и только тогда, когда регулярное множество замкнуто по сложению.

Доказательство леммы 2.1. Условие левой дистрибутивности имеет вид:

. (2.1)

Напомним, что в нашем случае операция умножения вводится следующим образом:

.

Следовательно, (2.1) примет вид:

.

В правой части равенства x можно вынести за скобку:

.

Так как x – произвольный элемент пространства, то:

.

Проверим теперь выполнение условия правой дистрибутивности:

. (2.2)

Следовательно, (2.2) примет вид:

.