Реферат: Построение полуполевых плоскостей

Равенство выполняется, следовательно, условие правой дистрибутивности выполняется.

Лемма 2.1 доказана.

Задача построения всех полуполевых плоскостей данного вида сводится к построению всех возможных регулярных множеств.

Так как все ненулевые матрицы невырожденные, то элементы первой строки однозначно определяются элементами второй строки матрицы:

,

где и - аддитивные функции двух аргументов из поля .

Если , то:

,

В нашем случае , тогда функции f (u, v ) и g (u, v ) таковы:

,

,

матрицы θ принимают вид:

.

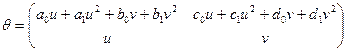Так как регулярное множество содержит единичную матрицу, то можно найти зависимость между коэффициентами, входящими в функции и. Нижняя строка единичной матрицы определена однозначно: u = 0, v = 1, следовательно:

, ,

, .

Была написана программа на языке С++, с помощью которой построено 56 полуполевых плоскостей порядка 16. Все соответствующие наборы коэффициентов приведены в приложении 1.

Для удобства дальнейшей работы с полем GF (4) его элементами будем считать 0,1,2,3, причем таблицы Кэли по сложению и умножению соответственно имеют вид:

+	0	1	2	3
0	0	1	2	3
1	1	0	3	2
2	2	3	0	1
3	3	2	1	0

*	0	1	2	3
0	0	0	0	0
1	0	1	2	3
2	0	2	3	1
3	0	3	1	2

2.2. Изоморфизм полуполевых плоскостей

На следующем этапе работы было необходимо разбить множество построенных плоскостей на классы плоскостей, изоморфных между собой. Для этой цели была применена теорема, доказанная в [3].

Теорема 2.2. Пусть π – спрэд V , π' – спрэд V' . Если σ – изоморфизм плоскости трансляций π (V ) на плоскость трансляций π' (V' ) такой, что 0^σ =0, тогда σ – биективное полулинейное отображение векторного пространства V на векторное пространство V' .

Или другими словами, плоскость π изоморфна плоскости π΄ найдется полулинейное отображение , сохраняющее компоненты расщепления,

.

Здесь σ – автоморфизм поля GF (4 ), А – невырожденная матрица, (x, xθ )π , а .

Установление изоморфизма заключается в определении зависимости между матрицами регулярных множеств (а точнее, между функциями, определяющими вид матриц).

Возможны случаи:

I) А=Е, σ – возведение в квадрат;

II) АЕ , σ= 1;

III) АЕ , σ – возведение в квадрат.

Так как мы рассматриваем полный список плоскостей, то достаточно установить наличие изоморфизмов типа I и II.

Рассмотрим случай I.

Пусть , а .

Известно:

.

Зная, что х =, , получаем:

,

.

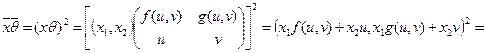
Таким образом, мы получили, что , т.е. все коэффициенты, стоящие при переменных u и v , возводятся в квадрат:

,

.

Рассмотрев первую плоскость, мы найдем изоморфную ей:

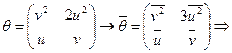первая плоскость изоморфна второй (12);

Дальнейшие вычисления показывают, что: (33), (44), (55), (66), (711), (812), (913), (1014), (1515), (1616), (1718), (1920), (2122), (2324), (2527), (2628), (2943), (3044), (3145), (3246), (3347), (3448), (3555), (3656), (3750), (3849), (3952), (4051), (4153), (4254).