Реферат: Построение полуполевых плоскостей
В этой теореме выражение вида 
означает 
.
Наш результат справедлив для линейных изоморфизмов полуполевых плоскостей.
Теорема 2.4. Если φ – линейный изоморфизм полуполевых плоскостей, то он может быть задан матрицей вида 
, где А4 – любая невырожденная матрица с элементами из GF (4),
≠ 0 – некоторая матрица изR .
Следует заметить, что в случае поля четного порядкадостаточно рассматривать матрицу 
с определителем равным 1. Покажем, что это действительно так.
Пусть матрица имеет вид:
A= 
и 
.
Тогда матрицу А можно записать в таком виде:
A= 
, и |A|=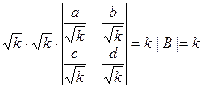 
,
.
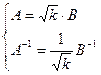
(т.к. в поле четного порядка квадратный корень из любого элемента извлекается однозначно, то мы имеем право сокращать).
Была написана программа на языке С++, рассчитывающая данный случай. В итоге мы получили 2 класса неизоморфных полуполевых плоскостей порядка 16:
I) {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56}
II) {17, 18, 31, 32, 45, 46}
или всего 2 плоскости: №1 и №17, и 17-я плоскость является дезарговой.Обозначим эти плоскости 
и 
соответственно.
Для плоскостей номер 1 и 17 матрицы имеют вид:
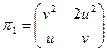и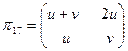 
.
Лемма 2.5. Для дезарговой плоскости (плоскость №17) регулярное множество является полем.
Доказательство леммы 2.5. Функции матрицы регулярного множества для плоскости №17 имеют вид:
, 
.
Проверим необходимые аксиомы:
1) Замкнутость по умножению:
,
.
Замкнутость выполняется.
2) Коммутативность умножения:
,
,
Коммутативность выполняется.
3) Ассоциативность умножения:
,
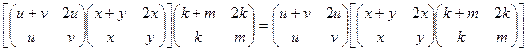Преобразуем левую часть равенства:
.
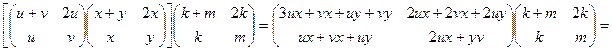
Преобразуем правую часть равенства:
.
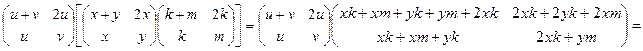
Ассоциативность выполняется.