Нехай дано рівняння

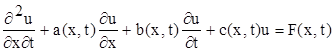(1.1)

Треба знайти розв’язок цього рівняння в області D(рис. 1)

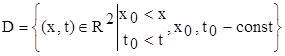
якщо задані крайові умови

u(x₀ , t) = j(t);

u(x, t₀ ) = y(x), (1.2)

при цьому функції j(t) та y(x) ддиференцьовані, та задовільнюють умові спряження

j(t₀ ) = y(x₀ ).

Така задача називається задачею з даними на характкристиках, або задачею Гурса.

D

Рис. 1

§2 . Приведення до канонічного вигляду

гіперболічного рівняння другого порядку

з двома незалежними змінними. Характеристики.

Розглянемо рівняння другого порядку з двома незалежними змінними

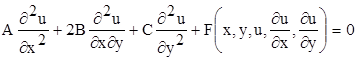, (2.1)

де коефіцієнти А, В та С – функції від x та y, які мають неперервні похідні до другого порядку включно у області WÌ R. За допомогою перетворення змінних

x = j(х, у), h = y(х, у),

яке припускає обернене перетворення, ми отримуємо нове рівняння, еквівалентне рівнянню (2.1). При цьому будемо мати

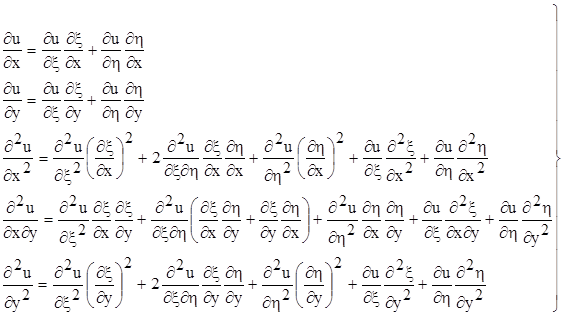
(2.2)

підставляючи значення похідних з(2.2) в (2.1), будемо мати:

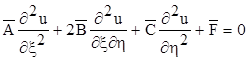, (2.3)

де

,

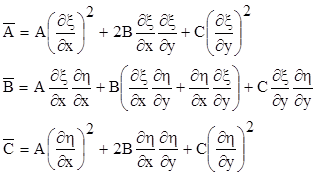а функція не залежить від других похідних. Замітимо, що якщо рівняння (2.1) було лінійно, то й рівняння (2.3) буде лінійним.

Рівняння (2.1) пов’язано з рівнянням:

Аdy² +2Вdydx+Сdx² =0 (2.4)

яке має назву рівнянням характеристичних змінних, а його інтеграли – характеристиками для рівняння (2.1).

(2.5)

Нехай j(x,y)=const є загальним інтегралом рівняння (2.4), тоді покладемо x=j(x,y) і коефіцієнт буде дорівнювати нулю, якщо y(x,y)= const другий, відмінний від першого інтеграл, то заміною h=y(x,y) ми доб’ємось, щоб =0.

Як видно з формули (2.5), рівняння (2.4) може мати різні розв’язки, один розв’язок або не мати розв’язків взагалі в залежності від знаку В² –АС.

Рівняння (2.1) у деякій точці М(x,y) будемо називати:

1) рівнянням гіперболічного типу, якщо В² –АС>0;

2) рівнянням параболічного типу, якщо В² –АС=0;

3) рівнянням параболічного типу, якщо В² –АС<0.

Відмітимо, що при довільній заміні змінних (2.2) виконується рівність

тобто при будь – якому перетворенні змінних, у якого якобіан відмінний від нуля, тип рівняння (2.1) не змінюється.

Розглянемо випадок, коли рівняння (2.1) має гіперболічний тип у деякій області GÌW. У цій області характеристичне рівняння має два різних загальних інтеграла j(x,y)=const та y(x,y)=const.

Зробимо заміну описану вище: x=j(x,y) та h=y(x,y), отримаємо:

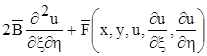
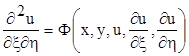(2.6)

де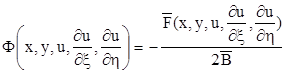

Рівняння (2.6) називається канонічною формою рівнянь гіпер-болічного типу. Покажемо, що характеристиками рівняння (2.6) будуть прямі, паралельні координатним осям, тобто x = const, h = const.

Для (2.6) рівнянням характеристичних змінних буде

dxdh = 0.

Звідки будемо мати

x = const, h = const.

§3 . Формула Остроградського-Гаусса.

Нехай P(x, y, z), Q(x, y, z) и R(x, y, z) – три функциї змінних x, y, z, які задані у області D’ и мають в ній неперервні похідні першого порядку по x, по y та по z.