Розглянемо рівняння (1.1). Оператори Lu, Mv, а також функції P₁ та P₂ будуть мати вигляд:

При цьому формула Гріна дає (нормаль внутрішня)

(5.2)

§6 . Побудова розв’язку.

Будувати розв’язок будемо методом Рімана, який полягає на використовуванні формули Гріна та дає рішення задачі (1.1) через граничні умови (1.2).

Нехай нам потрібно знайти значення функції u у деякій точці М області (x > x₀ , t > t₀ ) з координатами (x₁ , t₁ ).

Проведемо через точку М (рис. 2) з координатами (x₁ , t₁ ) дві прямі, які паралельні координатним осям. Нехай точка P(x₀ , t₁ ) – це точка перети-ну прямих x = x₀ та t = t₁ , а точка Q(x₁ , t₀ ) – точка перетину прямих

x = x₁ та t = t₀ . Прямі х = х₀ , х = х₁ , t = t₀ , t = t₁ як було показано раніше, є характеристиками рівняння (1.1). Область W буде являти собою прямокутник MPRQ. У цій області ми можемо застосувати метод Рімана для знаходження розв’язку.

Якщо враховувати, що обіг області W відбувається проти годинни-кової стрілки, так що обігаєма площа завжди залишається зліва, формулу (5.2) можна записати у вигляді

(5.2’)

З рисунку 2 бачимо, що при цьому

dx = cos(nt)dS,

dt = - cos(nx)dS.

За умови u(x₀ , t) = j(t) отримуємо:

= 0; = j’(t).

За умови u(x, t₀ ) = y(x), отримуємо:

= 0; = y’(x).

Рис. 2

Якщо застосувати формулу (5.2’) до прямокутника MPRQ, враховуючи, що на характеристиках QM та PR змінюється лише t, а на характерис-тиках MP та RQ змінюється лише x ,будемо мати:

(6.1)

Перетворимо кожен з інтегралів, який стоїть у правій частині (6.1):

(6.2.1)

(6.2.2)

(6.2.3)

(6.2.4)

Нехай тепер v(x, t, x₁ , t₁ ) – деяка функція, яка задовільнює умовам:

Mv = 0, (6.4)

, .

При цьому

v(x₁ , t₁ , x₁ , t₁ ) = 1,

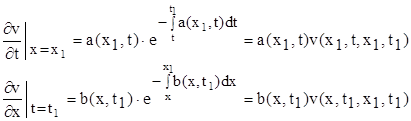(6.5)

Розв’язок v(x, t, x₁ , t₁ ) однорідного спряженого рівняння (6.4), який задовільнює умовам (6.5), називається функцією Рімана. Ця функція не залежить від початкових даних (1.2), та для неї точка (x, t) грає роль аргументу, а точка (x₁ , t₁ ) – роль параметру. Існування та єдиність такої функції v було доказано методом послідовних наближень.

Оскільки на прямій MP t = t₁ , а на прямій QM x = x₁ , то останні члени у формулах (6.2.1) та (6.2.2) обертаються в нуль, і ми отримаємо:

.

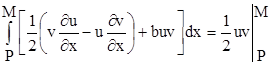
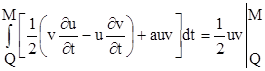Формулу (6.1) тепер можна записати у вигляді:

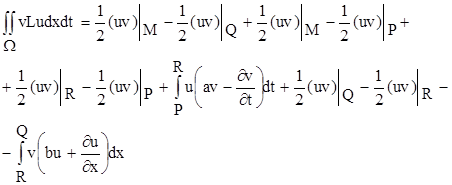
Приводячи подібні, та враховуючи, що v(x₁ , t₁ , x₁ , t₁ ) = 1, u(x₀ ,t) = j(t), u(x, t₀ ) = y(x) та ; = y’(x), маємо:

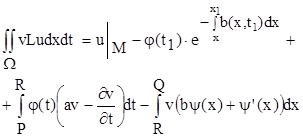
Звідки знаходимо розв’язок нашої задачі

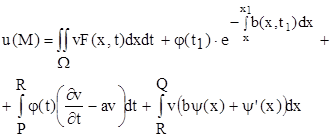(6.6)

Як ми бачимо, формула (6.6) дозволяє у явному вигляді написати розв’язок данної задачі, оскільки точку М(x₁ , t₁ ) ми вибрали довільно.

§7 . Деякі приклади на знаходження фунції Рімана.

Приклад 1.

Знайдемо функцію Рімана для рівняння

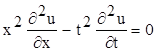. (7.1)

Зробивши заміну змінних

рівняння (7.1) приводиться до канонічного вигляду

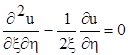
при цьому будемо мати a = 0, b = -.

Звернемося тепер до відшукання фунції Рімана v(x, h, x₁ , h₁ ). Згідно загальної теорії, вона повинна задовольняти спряженому рівнянню

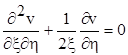(7.2)

та умовам на характеристиках, які проходять через точку (x₁ , h₁ ):

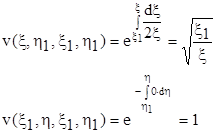(7.3)

неважко вконатися, що функція

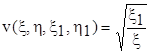
задовільнює як рівнянню (7.2), так і умовам (7.3), слід, це і є шукана функція Рімана.