Реферат: Построение решения задачи Гурса для телеграфного уравнения методом Римана

Знайдемо функцію Рімана для рівняння

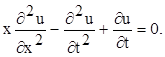(x > 0) (7.4)

приведемо рівняння (7.4) до канонічного вигляду, для чого складемо рівняння характерстик

xdt² – dx² = 0

це рівняння має два різних інтеграла

+ = C₁ , - = C₁ ,

слід, треба ввести нові змінні x та h за формулами

x = + , h = - (x >0)

приєднаємо до цих рівностей ще одну залежність

тоді рівняння (7.4) перетвориться до канонічного вигляду:

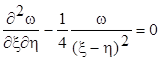
при цьому будемо мати a = 0, b = 0.

Для відшукання функії Рімана нам потрібно знайти частинний розв’язок спряженого рівняння

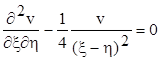(7.5)

який задовольняв би слідуючим умовам на характеристиках, проведених через точку (x₁ , h₁ )

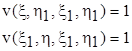(7.6)

Будемо шукати розв’язок рівняння (7.1) у вигляді v = G(s), де

s =.

Тоді для G(s) ми отримаємо слідуюче рівняння:

s(1-s)G’’(s) + (1-2s)G’(s) - G(s) = 0

Це рівняння частинним випадком гіпер геометрічного рівняння Гаусса

s(1-s)y’’ + [g - (1 + a + b)s]y’ - aby = 0

при a = b = , g = 1.

Рівняння Гаусса припускає частинний розв’язок у вигляді гіпергеометрічного ряду

який збігається абсолютно при |s| < 1.

Звідки ясно, що взявши

v = G(s) = F= 1 +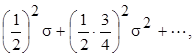

ми задовільним рівнянню (7.5) та усмовам (7.6). Слід, функція

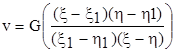
і є функцією Рімана.

Приклад 3.

Знайдемо функцію Рімана для телеграфного рівняння

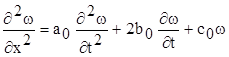
якщо ввести нову функцію u(x, t) поклавши

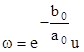(7.7)

то рівняння (7.7) більш просту форму

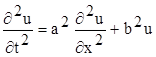, (7.8)

де a = , b = .

За допомогою заміни змінних

x = (x + at), h = (x - at)

приведемо рівняння (7.8) до канонічного вигляду

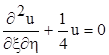
при цьому маємо a = b = 0.

Функція Рімана повинна задовільнювати спряженому рівнянню

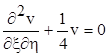, (7.9)

та на характеристиках x = x₁ , h = h₁ дорівнює одиниці.