Реферат: Предел и непрерывность функций нескольких переменных

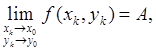(2)

какова бы ни была стремящаяся к (х ₀ , у ₀ ) последовательность точек (x_k , y_k ).

Так же, как в случае функции одной переменной, можно ввести другое эквивалентное определение предела функции двух переменных: функция f имеет в точке (х ₀ , у ₀ ) предел, равный А , если она определена в некоторой окрестности точки (х ₀ , у ₀ ) за исключением, быть может, самой этой точки, и для любого ε > 0 найдется такое δ > 0, что

| f ( x , y ) – A | < ε(3)

для всех ( x , y ) , удовлетворяющих неравенствам

0 < < δ. (4)

Это определение, в свою очередь, эквивалентно следующему: для любого ε > 0 найдется δ-окрестность точки (х ₀ , у ₀ ) такая, что для всех (x , y ) из этой окрестности, отличных от (х ₀ , у ₀ ), выполняется неравенство (3).

Так как координаты произвольной точки (x , y ) окрестности точки (х ₀ , у ₀ ) можно записать в виде х = х ₀ + Δх , у = у ₀ + Δу , то равенство (1) эквивалентно следующему равенству:

Рассмотрим некоторую функции, заданную в окрестности точки (х ₀ , у ₀ ), кроме, быть может, самой этой точки.

Пусть ω = (ω_х , ω_у ) – произвольный вектор длины единица (|ω|² = ω_х ² + ω_у ² = 1) и t > 0 – скаляр. Точки вида

(х ₀ + t ω_х , y ₀ + t ω_у ) (0 < t )

образуют луч, выходящий из (х ₀ , у ₀ ) в направлении вектора ω. Для каждого ω можно рассматривать функцию

f (х ₀ + t ω_х , y ₀ + t ω_у ) (0 < t < δ)

от скалярной переменной t , где δ – достаточно малое число.

Предел этой функции (одной переменной t )

f (х ₀ + t ω_х , y ₀ + t ω_у ),

если он существует, естественно называть пределом f в точке (х ₀ , у ₀ ) по направлению ω.

Пример 1. Функции

определены на плоскости (x , y ) за исключением точки х ₀ = 0, у ₀ = 0. Имеем (учесть, что и ):

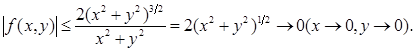
Отсюда

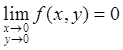
(для ε > 0 полагаем δ = ε/2 и тогда |f ( x , y ) | < ε, если < δ).

Далее, считая, что k – постоянная, имеем для y = kx равенство

из которого видно, что предел φ в точке (0, 0) по разным направлениям вообще различен (единичный вектор луча y = kx , х > 0, имеет вид

).