Реферат: Предел и непрерывность функций нескольких переменных

(х ⁴ + у ² ≠ 0).

Данная функция в точке (0, 0) на любой прямой y = kx , проходящей через начало координат, имеет предел, равный нулю:

при х → 0.

Однако эта функция не имеет предела в точки (0, 0), ибо при у = х ²

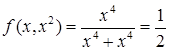и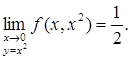

Будем писать 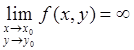, если функция f определена в некоторой окрестности точки (х ₀ , у ₀ ), за исключением, быть может, самой точки (х ₀ , у ₀ ) и для всякого N > 0 найдется δ > 0 такое, что

|f ( x , y ) | > N ,

коль скоро 0 < < δ.

Можно также говорить о пределе f , когда х , у → ∞:

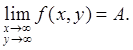(5)

Например, в случае конечного числа А равенство (5) надо понимать в том смысле, что для всякого ε > 0 найдется такое N > 0, что для всех х , у , для которых |x | > N , |y | > N , функция f определена и имеет место неравенство

|f ( x , y ) – А | < ε.

Справедливы равенства

(6)

(7)

(8)

где может быть х → ∞, у → ∞. При этом, как обычно, пределы (конечные) в их левых частях существуют, если существуют пределы f и φ.

Докажем для примера (7).

Пусть (x_k , y_k ) → (х ₀ , у ₀ ) ((x_k , y_k ) ≠ (х ₀ , у ₀ )); тогда

(9)

Таким образом, предел в левой части (9) существует и равен правой части (9), а так как последовательность (x_k , y_k ) стремится к (х ₀ , у ₀ ) по любому закону, то этот предел равен пределу функции f ( x , y ) ∙φ ( x , y ) в точке (х ₀ , у ₀ ).

Теорема. если функция f ( x , y ) имеет предел, не равный нулю в точке (х ₀ , у ₀ ), т.е.

то существует δ > 0 такое, что для всех х , у , удовлетворяющих неравенствам

0 < < δ, (10)

она удовлетворяет неравенству

(12)

Поэтому для таких ( x , y )