Реферат: Предел и непрерывность функций нескольких переменных
Связное открытое множество называется областью.
Теорема. Пусть функция f ( x ) определена и непрерывна на Rn (во всех точках Rn ). Тогда множество G точек х , где она удовлетворяет неравенству
f ( x ) > с (или f ( x ) < с ), какова бы ни была постоянная с , есть открытое множество.
В самом деле, функция F ( x ) = f ( x ) – с непрерывна на Rn , и множество всех точек х , где F ( x ) > 0, совпадает с G . Пусть х 0 ![]() G , тогда существует шар
G , тогда существует шар
| х – х 0 | < δ,
на котором F ( x ) > 0, т.е. он принадлежит к G и точка х 0 ![]() G – внутренняя для G .
G – внутренняя для G .
Случай с f ( x ) < с доказывается аналогично.
Таким образом, функция нескольких переменных f (М) называется непрерывной в точке М 0 , если она удовлетворяет следующим трем условиям:
а) функция f (М) определена в точке М 0 и вблизи этой точки;
б) существует предел ![]() ;
;
в) ![]()
Если в точке М 0 нарушено хотя бы одно из этих условий, то функция в этой точке терпит разрыв. Точки разрыв могут образовывать линии разрыва, поверхность разрыва и т. д. Функция f (М) называется непрерывной в области G , если она непрерывна в каждой точке этой области.
Пример 1. Найти точки разрыва функции: z = ln ( x 2 + y 2 ) .
Решение. Функция z = ln ( x 2 + y 2 ) терпит разрыв в точке х = 0, у = 0. Следовательно, точка О (0, 0) является точкой разрыва.
Пример 2. Найти точки разрыва функции: 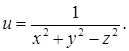
Решение. Функция не определена в точках, в которых знаменатель обращается в нуль, т.е. x 2 + y 2 – z 2 = 0. Следовательно, поверхность конуса
x 2 + y 2 = z 2 является поверхностью разрыва.
Заключение
Начальные сведения о пределах и непрерывности встречаются в школьном курсе математики.
В курсе математического анализа понятие предела является одним из основных. С помощью предела вводятся производная и определенный интеграл; пределы же являются основным средством в построении теории рядов. Понятие предела, впервые появившееся в 17 веке в работах Ньютона, используется и получает дальнейшее развитие в теории рядов. В этом разделе анализа исследуются вопросы, связанные с суммой бесконечной последовательности величин (как постоянных, так и функций).
Непрерывность функции дает представление о ее графике. Это означает, что график есть сплошная линия, а не состоит из отдельных разрозненных участков. Это свойство функции находит широкое применение в сфере экономики.
Поэтому понятия предела и непрерывности играют важную роль в исследовании функций нескольких переменных.
Список использованной литературы
1. Бугров Я.С., Никольский С.М. Высшая математика: Учебник для вузов. Том 2: Дифференциальное и интегральное исчисление. Москва: Дрофа, 2004 год, 512 с.
2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридма М.Н. Высшая математика для экономистов. Москва: Юнити, 2000 год, 271 с.
3. Черненко В.Д. Высшая математика в примерах и задачах. Учебное пособие для вузов. Санкт-Петербург: Политехника, 2003 год, 703 с.
4. http://elib.ispu.ru/library/math/sem2/index.html
5. http://www.academiaxxi.ru/WWW_Books/HM/Fn/toc.htm