Реферат: Преобразование Фурье

(6)

так как , то интеграл (6) сходится равномерно при t³0, и дифференцирование законно. Совершенно так же доказывается бесконечная дифференцируемость функции u( x, t) по t и x .

Дифференцируя (5) дважды по x, устанавливаем:

(7)

Из формул (6),(7) вытекает, что функция u( x, t) удовлетворяет уравнению (1). Справедливость условия (2) очевидна. Теорема доказана.

§4. Фундаментальное решение уравнения теплопроводности.

Преобразуем формулу (5) к более удобному ”явному” виду. Для этого запишем ее в интегралах

меняем порядок интегрирования

(8)

В формуле (8) внутренний интеграл есть преобразование Фурье от функции при значении аргумента –( x- z) , поэтому из (9.2) имеем

Подставляя это в (8), получим

(9)

Функцию

называют фундаментальным решением уравнения теплопроводности. Легко проверяются следующие свойства этой функции:

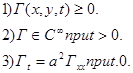
§5. Решение задачи с непрерывной ограниченной начальной функцией.

Теорема 3. Пусть j(z) ограничена и непрерывна на вещественной оси. Тогда формула (9) дает решение задачи (1),(2).

Доказательство. Продифференцируем (9) под знаком интеграла

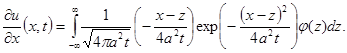(10)

Чтобы обосновать законность такого дифференцирования, достаточно показать равномерную сходимость по x интеграла (10), для чего произведем замену

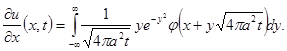
Из ограниченности функции j следует равномерная сходимость интеграла как по xÎR, так и по t>e.

Совершенно так же доказывается бесконечная дифференцируемость функции u(x, t) по x и t при t>0. Из свойства 3) фундаментального решения следует, что u есть решение уравнения (1).

Для доказательства (2) снова сделаем замену переменной интегрирования в (9):

Так как последний интеграл сходится равномерно по x и t, то возможен предельный переход под знаком интеграла

Теорема доказана.

§6. Единственность решения в классе ограниченных функций.