Реферат: Применение экономико-математического моделирования для обоснования
1.2 Первая и вторая теорема двойственности.
Первая теорема двойственности
Основная теорема двойственности линейного программирования. Пусть рассматривается пара двойственных задач:
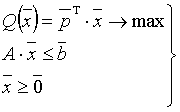(1) 
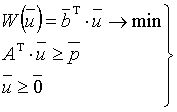(2)
Если одна из этих задач обладает оптимальным решением, то и двойственная к ней задача также имеет оптимальное решение. Причем экстремальные значения соответствующих линейных форм равны: 
.
Если же у одной из этих задач линейная форма не ограничена, то двойственная к ней задача противоречива.
Доказательство: Пусть основная задача (1) имеет конечное решение и получена окончательная симплексная таблица:
Так как данная таблица, по предположению, соответствует оптимальному решению задачи (1), то 
и 
. При этом 
достигается при 
.
Рассмотрим полученную таблицу двойственной задачи. Полагая значения переменных слева (небазисных) равными нулю:
,
найдем 
, …, 
, 
, …, 
. Следовательно, получено опорное решение:
, …, 
, 
, …, 
.
Из последнего столбца,
в точке
будет минимальным в силу того, что 
, 
. Следовательно, .
Пусть теперь линейная форма прямой задачи неограничена, т.е. для некоторой верхней переменной, например, 
соответствующий коэффициент 
, а все коэффициенты этого столбца симплексной таблицы неположительны: 
, 
, …, 
. Тогда из таблицы для двойственной задачи:
,
то есть система ограничений двойственной задачи противоречива. Так как из неотрицательности 
следует неположительность 
(нельзя сделать ее положительной). То есть, система несовместна.
Теорема доказана.
Вторая теорема двойственности
Если хотя бы одно оптимальное решение одной из двойственных задач обращает 
-е ограничение этой задачи в строгое неравенство, то -я компонента (т.е. 
или 
) каждого оптимального решения второй двойственной задачи равна нулю.
Если же -я компонента хотя бы одного оптимального решения одной из двойственных задач положительна, то каждое оптимальное решение другой двойственной задачи обращает -е ограничение в строгое равенство.
Т.е. оптимальные решения 
и 
пары двойственных задач удовлетворяют условиям
(1)
(2)
Доказательство: Пусть и – оптимальные решения пары двойственных задач. Тогда для
,