Реферат: Применение экономико-математического моделирования для обоснования
Оптимальное значение переменных соответствует элементам из столбца «b» последней симплексной таблицы, а максимальное значение целевой функции содержимому ячейки (сбазис ,b).
2.3 Двойственные задачи
Прежде чем строить двойственную задачу, предварительно исходную задачу линейного программирования нужно привести к виду, где все ограничения неравенства имеют один тип, а целевая функция - направление, противоположное типу ограничений неравенств.
Правила построения двойственной задачи.
1. Целевая функция в двойственной задаче меняет своё направление на противоположное.
2. Количество двойственных переменных равно количеству основных ограничений исходной задачи.
3. Двойственная переменная, соответствующая ограничению равенству, является неограниченной по знаку, а соответствующая ограничению неравенству – неотрицательной.
4. Вектор правых частей ограничений исходной задачи является вектором коэффициентов целевой функции в двойственной задаче.
5. Вектор коэффициентов целевой функции исходной задачи является вектором правых частей ограничений в двойственной задаче.
6. Матрица коэффициентов ограничений двойственной задачи – это транспонированная матрица коэффициентов исходной задачи, т.е. строка коэффициентов исходной задачи, является столбцом коэффициентов двойственной задачи.
7. Неотрицательным переменным исходной задачи соответствуют ограничения неравенства в двойственной задаче, причем тип неравенства меняется на противоположный, по сравнению с исходной задачей. А неограниченной переменной исходной задачи соответствует ограничение равенство в двойственной задаче.
Соотношение двойственности является симметричным, т.е. двойственная задача по отношению к двойственной совпадает с исходной.
Если исходная задача линейного программирования записана в стандартном виде: (с, х)→ max
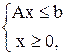 (4.1)
(4.1)
то соответствующая ей двойственная задача записывается следующим образом:
(b, y)→min
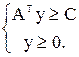 (4.2)
(4.2)
Для следующей задачи линейного программирования построим двойственную задачу.
3x1 + 3x2 – 4x3 → max
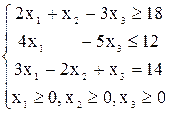
![]()
![]() -2х1 - х2 + 3х3 ≤ -18 у1
-2х1 - х2 + 3х3 ≤ -18 у1
4х1 - 5 х3 ≤ 12 у2
3х1 - 2 х2 + х3 = 14 у3
х1 ≥ 0; х2 ≥ 0; х3 ≥ 0
Вводом двойственные переменные
![]() -18у1 +12у2 +14у3 min
-18у1 +12у2 +14у3 min
![]() -2у1 + 4у2 + 3у 3 ≥ 3
-2у1 + 4у2 + 3у 3 ≥ 3
-у1 - 2у3 ≥3
3у1 - 5у2 + у3 ≥ -4
у1 ≥0; у2 ≥0