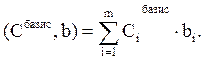Реферат: Применение экономико-математического моделирования для обоснования

Основные положения, на которых базируется симплекс – метод

1. Каждая вершина многогранника допустимых решений обладает следующими свойствами:

- m её координат имеют значения ≥0 (их называют базисными переменными);

- остальные (n - m) координат равны нулю (их называют свободными переменными);

- вектор – столбцы матрицы коэффициентов А, соответствующие базисным переменным вершины являются линейно независимыми, т.е. с- помощью линейных преобразований их можно привести к единичной матрице.

2. Соседние вершины многогранника допустимых решений отличаются только одной базисной переменной.

3. Переход из одной вершины в другую осуществляется с помощью метода последовательного исключения неизвестных, который называется методом Жордана-Гаусса. В результате чего из базисного решения выводим одну переменную, а вводим другую. Причём, из свободных переменных, не вошедших в базис, вводим ту, которая больше всех уменьшает значение целевой функции. А из базисных переменных выводим ту, которая не нарушает условия неотрицательности базисных переменных у новой вершины. При этом вектор – столбцы матрицы ограничений А, соответствующие новой вершине, так же будет линейно независимыми, т.е. образовывать единичную матрицу.

Алгоритм симплекс – метода

1. Находим первое опорное решение (угловую точку).

2. Составляем симплексную таблицу (см. рис.3.1).

3. Выясняем, имеется ли хотя бы одно отрицательное число ∆j. Если таких чисел нет, то найденное опорное решение является оптимальным. Если же среди чисел ∆_j имеются отрицательные, то либо переходят к новому опорному решению, либо устанавливают неразрешимость задачи, когда все коэффициенты столбца матрицы ограничений А, соответствующего отрицательному ∆_j , тоже отрицательны.

4. Направляющий столбец (номер вводимой в базис переменной) определяем наибольшим по абсолютной величине отрицательным числом ∆_j . Пусть это будет к-ый столбец.

5. Направляющая строка (номер выводимой из базиса переменной) соответствует минимальному из всех соотношений для положительных значений а_ik . Пусть это l – ая строка.

6. По методу Жордана – Гаусса исключаем переменную Хк из всех ограничений, кроме l –ого, где эта переменная должна быть с коэффициентом 1. Строим, новею симплекс – таблицу.

7. Переходим к этапу 3.

Для поиска первого опорного решения можно использовать следующие методы:

- метод естественного базиса,

- метод искусственного базиса.

Метод естественного базиса применяется для задач линейного программирования, записанных в виде (3.2), где все ограничения неравенства имеют тип "≤" и элементы вектора правых частей ограничений неотрицательны.

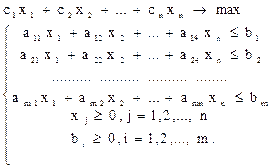(3.2)

В этом случае задачу (3.2) приводим к каноническому виду (3.3), вводя в левую часть каждого ограничения неравенства самостоятельную переменную, которые и будут образовывать естественный базис.

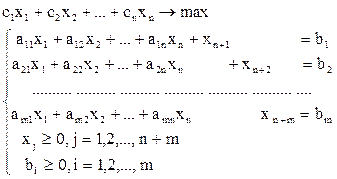(3.3)

Метод искусственного базиса применяется для задач, заданных в каноническом виде, или с ограничениями смешанного типа. Если в задаче ограничения смешанного типа, то её сначала преобразуем к каноническому виду (3.1), причем нужно отслеживать, чтобы элементы вектора правых частей были неотрицательными, а затем в каждое ограничение равенство водим по самостоятельной переменной y_j , которые и будут образовывать искусственный базис. При этом в целевой функции переменные искусственного базиса записываются с большими отрицательными коэффициентами. В результате преобразований получим задачу вида 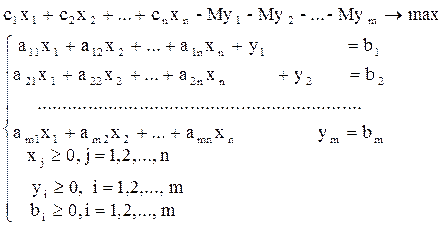(3.4).

(3.4)

базис	Сбазис	b	С1	С2	…	Сn
			Х1	Х2	…	Xn
X1 базис	С1 базис	b1	a11	a12	…	a1 n
Х2 базис	С2 базис	b2	a21	a22	…	a2 n
…	…	…	…	…	…	…
Хм базис	Сmбазис	bm	am 1	am 2	…	amn
(Cбазис ,b)			…

Рис. 3.1. Симплексная таблица

Правила заполнения первой симплексной таблицы

1. Вместо С₁ , С₂ , …, С_n записываем соответствующие коэффициенты целевой функции.

2. Вместо а_ij записываем коэффициенты при неизвестных из основных ограничений задачи.

3. Вместо Х_i ^базис записываем имена переменных, вошедших в базис, в той последовательности, в которой они образуют единичную матрицу.

4. Вместо С_i ^базис записываем коэффициенты целевой функции при соответствующих базисных переменных.

5. Вместо b_i записываем элементы вектора правых частей задачи.

6.