Реферат: Применение методов линейного программирования в военном деле. Симплекс-метод

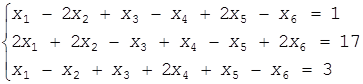
Нужно данную систему разрешить относительно переменных x₁ , x₂ , x₃ . Следовательно свободными переменными будут x₄ , x₅ , x₆ . Напишем таблицу, соответствующую данной системе уравнений.

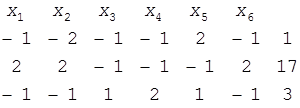
Решим систему относительно x₁ с помощью первого уравнения. За разрешающий элемент принимаем первый элемент первой строки, и подвергнем таблицу S-преобразованию. Получим новую таблицу, где первая строка переписывается, в первом столбце записываются нули, а остальные элементы вычисляются по D-правилу.

Этой таблице соответствует система уравнений, разрешенная относительно x₁ (x₁ входит только в первое уравнение). Исключить x₂ удобнее с помощью третьего уравнения, так как коэффициент при x₂ в третьем уравнении равен единице. Принимаем его за разрешающий элемент. Пишем новую таблицу

Система уравнений, соответствующая этой таблице, разрешена относительно x₁ и x₂ (x₁ входит только в первое уравнение, а x₂ только в третье).

Для разрешения системы относительно x₃ за разрешающий элемент берем коэффициент при x₃ во втором уравнении. Новая таблица имеет вид

Последняя таблица соответствует системе, решенной относительно базисных переменных x₁ , x₂ , x₃ . Полагая свободные переменные x₄ , x₅ , x₆ равными нулю, получим уравнения:

-3x₁ =-18, откуда x₁ =6

-3x₂ =-6, откуда x₂ =2

-3x₃ =3, откуда x₃ =-1

Совокупность чисел x₁ =6, x₂ =2, x₃ =-1, x₄ =0, x₅ =0, x₆ =0 есть одно из решений данной системы. Оно не принадлежит к области допустимых решений, так как одна из координат x₃ отрицательна.

Для решения задачи линейного программирования важно уметь находить неотрицательные (опорные) решения данной системы уравнений.

Правило выбора разрешающего элемента при отыскании неотрицательного решения системы уравнений.

Пусть дана система уравнений

(3.36)

В системе (3.36) свободные члены можно считать неотрицательными, так как в обеих частях уравнения всегда можно поменять знаки.

Если при выполнении симплекс преобразований при переходе от одной системы к другой будем следить за тем, чтобы разрешающие элементы были положительными, то на последнем этапе разрешения системы относительно базисных переменных получим систему вида (3.34) и по формулам (3.35) найдем неотрицательные значения базисных переменных. Составляем отношения свободных членов b_k к положительным элементам a_kj разрешающего столбца и среди чисел выбираем наименьшее значение. Если наименьшее значение достигается при k=i, то i-номер разрешающей строки, а разрешающим элементом будет a_ij .

Рассмотрим пример отыскания неотрицательных решений системы уравнений.

Пример. Найти неотрицательное решение системы уравнений

Пишем таблицу, соответствующую данной системе

Пробуем разрешить эту систему относительно x₁ , т.е. переменную x₁ будем считать базисной переменной. Первый столбец будет базисным столбцом. Составляем отношения свободных членов к положительным элементам первого столбца 10/2=5; 4/7. Наименьшее из этих чисел 4/7. Числа 4 и 7 находятся во второй строке. Следовательно разрешающей строкой будет вторая строка и разрешающим элементом число 7. Выполняя симплекс преобразование, получим новую таблицу

Этой таблице соответствует система уравнений, разрешенная относительно базисной переменной x₁ . Так как обе части любого уравнения системы можно умножать и делить на любое постоянное число (система при этом будет эквивалентна прежней), то если строки таблицы имеют общий множитель, на него можно сократить. Последняя строка предыдущей таблицы имеет общий множитель 7; сокращая на него, получим таблицу