Реферат: Применение методов линейного программирования в военном деле. Симплекс-метод

Задачи оптимального распределения средств поражения в общем виде формулируются так: имеется некоторое количество средств поражения и целей. Требуется так распределить средства поражения по целям, чтобы общий эффект применения был в определенном смысле оптимален.

Поражение противника является одним из важных элементов боевых действий. Поэтому решение задач на поражение является важным этапом при планировании и управлении боевыми действиями.

Различают два основных типа задач целераспределения:

- для средств поражения, находящихся в обороне;

- для средств поражения нападения;

Распределение средств поражения обороны осуществляется в ходе боевых действий, выявляемые цели и возникающие условия заранее неизвестны и во многом определяются противником. Расчеты нужно производить очень быстро, что возможно при наличии современных вычислительных средств.

Распределение средств нападения по выявленным целям может быть спланировано заранее на основе расчетов. Однако резкой границы между этими вариантами нет потому, что в обоих случаях выявляются новые цели, изменяются условия и потребуется производить перерасчеты.

Задача распределения средств поражения при ведении боевых действий в полной мере очень сложна и требует учета большого числа факторов. Некоторые же частные задачи успешно решаются с помощью линейного программирования.

Рассмотрим первую из таких задач. Имеется m различных средств поражения и n целей. Принимаются следующие допущения:

- число средств поражения не превосходит числа целей m£n;

- цели имеют разную важность, определяемую коэффициентом важности k_j (j=1,2,…,n);

- за каждой целью не может быть закреплено более одного средства поражения, то есть должно быть обстреляно максимальное число целей;

- известны вероятности p_ij поражения i-ым средством j-ой цели, которые составляют таблицу вероятностей поражения :

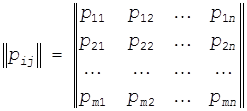(5)

Таблица вероятности поражения вычисляется по соответствующим формулам теории стрельбы.

Закрепление или не закрепление i-того средства поражения за j-той целью выражается величиной x_ij , принимающей значение 1, когда имеется закрепление, и 0, когда его нет.

План распределения средств по целям будет определяться таблицей (таблицей 1). За критерий эффективности в общем случае выберем взвешенное математическое описание числа уничтоженных целей, которое определяется выражением

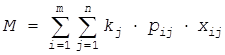(6)

где k_j (j=1,2,…,m) – коэффициенты, определяющие важность целей. Если цели имеют одинаковую важность, то k₁ =k₂ =…=k_m =1. При этих значениях выражение (6) является математическим ожиданием числа уничтоженных целей. Требование, чтобы каждое средство было закреплено за какой либо целью, определяется выражениями

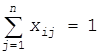(i=1,2,…,m) (7)

Условия, что за каждой целью закрепляется не более одного средства поражения, определяются выражением

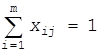(j=1,2,…,n) (8)

В случае знака равенства во всех выражениях (8) имеет место m=n, в противном случае m<n. Первая задача целераспределения может быть сформулирована следующим образом.

Найти такие целые значения x_ij ³0 (найти такой план), удовлетворяющие условиям (7) и (8), которые обращают критерий эффективности (6) в максимум.

Как видно, эта задача линейного программирования, причем транспортного типа. В отличие от задачи на перевозку здесь ищутся значения x_ij , принимающие только два возможных значения: 0 и 1.

При малых m и n задачи целераспределения могут решаться путем элементарных расчетов и рассуждений.

Задача. Разведкой обнаружены три равноценные цели противника. Для их уничтожения выделяется командованием три средства поражения. Известны вероятности поражения каждой цели любым средством (таблица 3).

Таблица 3.

Средства поражения

« 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 456 Бесплатно скачать Реферат: Применение методов линейного программирования в военном деле. Симплекс-метод >>> Скачать <<< Меню Поиск