Реферат: Применение методов линейного программирования в военном деле. Симплекс-метод

Количество целей

1

1

1

Требуется сформулировать задачу линейного программирования по критерию математического ожидания для данных условий и определить оптимальный план целераспределения.

Решение. Критерий эффективности в этой задаче согласно формуле (6) определяем выражением:

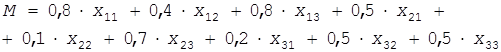(9)

Здесь положено k₁ =k₂ =k₃ =1, т.к. все цели равноценны. Выражения (7) и (8) для условия задачи будут иметь вид:

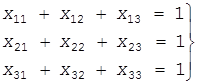(10)

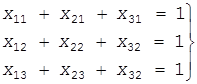(11)

Найти такие целые положительные корни x_ij уравнений (10) и (11), при которых критерий эффективности (9) примет максимальное значение.

Для определения оптимального плана найдем в столбцах таблицы 3 максимальные значения вероятностей и отметим их звездочками. Очевидно, что за второй целью нужно закрепить 3-е средство (x₃₂ =1). Первое средство одинаково целесообразно закрепить за 1-ой или 3-ей целью. Но так как ближайшее значение к максимальной вероятности для 3-ей цели больше, чем для 1-ой, то целесообразно 1-ое средство закрепить за 1-ой целью (x₁₁ =1), a 2-oe средство за 3-ей целью (x₂₃ =1).

Максимальное значение математического ожидания числа пораженных целей будет равно:

При оптимальном плане будет поражено в среднем две цели. Для сравнения рассмотрим следующий план: x₁₃ =1, x₂₂ =1 и x₃₁ =1. При этом плане средние потери будут равны

Таким образом, только за счет оптимального целераспределения эффективность средств поражения может быть значительно повышена (в данном примере почти в два раза). Этот факт имеет не только экономическое значение, но и повышает оперативность выполнения задачи на поражение цели.

III. СИМПЛЕКС-МЕТОД.

Симплекс-метод решения задачи линейного программирования. Пусть дана система n линейных уравнений с m переменными (n<m).

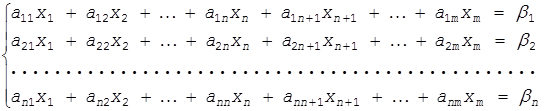(3.22)

Предположим, что среди детерминантов n-го порядка, которые можно составить из коэффициентов n первых столбцов, отличен от нуля.

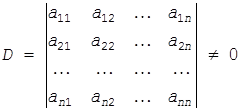
Тогда систему (3.22) можно разрешить относительно переменных x₁ , x₂ , …,x_n которые, как и раньше, будем называть базисными переменными. В результате решения системы (3.22) базисные переменные будут выражены через остальные переменные x_n+1 , x_n+2 , …, x_m , называемые свободными. Число свободных переменных k=m-n. Мы имеем решение системы (3.22) в виде:

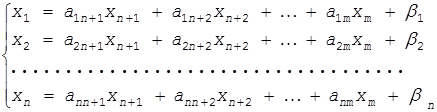(3.23)

Свободные переменные остаются произвольными. Давая им различные значения, получим все решения системы (3.22). Одно из решений найдем, если все свободные переменные приравняем к нулю. Тогда получим:

x₁ =b₁ , x₂ =b₂ , …, x_n =b_n ; x_n+1 =x_n+2 =…=x_m =0

Если все числа b₁ , b₁ , …,b_n неотрицательны, то мы будем иметь неотрицательное решение системы (3.22), соответствующее угловой точке (вершине) многогранника неотрицательных решений, это так называемое опорное решение.

Решить систему относительно базисных переменных x₁ , x₂ , …,x_n , используя свойства определителей n-го порядка, очень удобно. Мы будем решать эту систему путем последовательного исключения неизвестных.

Запишем в виде таблицы коэффициенты уравнений (3.24) и элемент a₁₁ заключим в рамку