Реферат: Применение методов линейного программирования в военном деле. Симплекс-метод
x32 =250
3*
x33 =350
5*
x34 =0
4
60
Потребность в ГСМ
350
450
400
500
Выбор планов зависит от запасов ГСМ на складах и потребностей в нем соединений, что математически определяется выражениями:
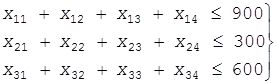 (21 )
(21 )
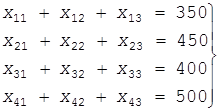 (31 )
(31 )
Суммарные расходы на перевозку ГСМ определяются линейными выражениями:
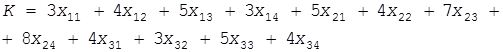 (41 )
(41 )
Требуется определить такие значения xij (выбрать такой план) удовлетворяющий выражениям (21 ) и (31 ), которые критерий эффективности обращают в минимум. Так формулируется задача линейного программирования для данных условий.
Эта задача решается элементарными подсчетами и рассуждениями.
Отметим в столбцах звездочками минимальные значения стоимости перевозки одной тонны ГСМ. В каждое соединение нужно планировать доставку из того склада, для которого эта стоимость будет наименьшей или близкой к ней, но с учетом расходов на доставку ГСМ и в другие соединения. Очевидно, в 1-е и 4-е соединение целесообразно завозить ГСМ полностью из 1-го склада, поэтому целесообразно выбрать x11 =350, x14 =500. Во второе соединение выгодно доставить горючее целиком с 3-го склада. Но тогда будут большие расходы при доставке ГСМ в 3-е соединение из 2-го склада. Поэтому целесообразно выбрать x13 =50, x33 =350, т.е. завести горючее в 3-е соединение с 1-го и 3-го складов, а 200 т. для 2-го соединения завести из склада, x22 =200, x32 =250. Результаты расчетов занесены в таблице 2, по которой удобно проверить выполнение условий (21 ), (31 ), найдя суммы xij по строкам и столбцам.
При таком плане расходы будут минимальными:
![]()
Для сравнения, какую можно иметь экономию в средствах, выбрав оптимальный план, рассмотрим один из возможных планов:
x11 =350, x12 =450, x13 =x14 =0, x21 =x22 =x23 =0,
x24 =300, x31 =x32 =0, x33 =400, x34 =200
При этом плане стоимость перевозок будет равна:
![]()
Она больше на 1950 единиц Kmin , что составляет более чем 30%.
Полученное оптимальное решение является основой для применения объективного решения на снабжение ГСМ соединений с учетом конкретной обстановки.