Реферат: Расчет характеристик участка линейного нефтепровода

= 0 (9)

Раскрывая полную производную по времени в подынтегральном выражении по правилу

(10)

приведем уравнение (9) к виду

(11)

В силу произвольности выбора множества W из (9) следует, что подынтегральное выражение должно быть равно нулю.

(12)

Эта формула называется законом сохранения массы в дифференциальной форме.

Для одномерного течения жидкости уравнение примет вид

(13)

Закон сохранения количества движения.

Этот закон гласит: скорость изменения количества движения любой части материальной системы, находящейся в движении, равна сумме всех внешних сил. В математическом виде этот закон запишется так:

(1)

где (2)

F_v – силы обусловленные силовыми полями

F_s – силы действующие на единицу поверхности.

Подставив (2) в (1) получим интегральную форму записи закона сохранения количества движения

. (3)

Это векторное уравнение эквивалентно системе из трех уравнений, отражающих закон сохранения количества движения по каждой из координат х₁ , х₂ , х₃

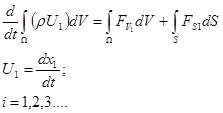(4)

Пользуясь правилами дифференцирования интеграла, взятого по изменяющемуся объему и объединяя два слагаемых, получим

. (5)

Учитывая приведем (5) к виду

. (6)

Поскольку это равенство справедливо при произвольном объеме подынтегральное выражение (6) должно быть равно нулю

. (7)

Выражение (7) есть дифференциальная форма записи закона сохранения количества движения.

Для одномерного случая, когда все составляющие сил и скоростей по всем направлениям, кроме оси х₁ , равны нулю, уравнения (5) и (7) примет вид

.
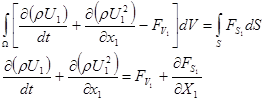