Реферат: Решение уравнений, неравенств, систем с параметром (алгебра и начала анализа)

Если а Î , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.

Ответ:

Если а Î (-¥;-1]È(1;+¥)È, то ;

Если а Î , то , ;

Если а Î , то решений нет.

II. Найти все значения параметра а, при которых уравнение имеет три различных корня.

Решение.

Переписав уравнение в виде и рассмотрев пару функций , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции , при которых он имеет точно три точки пересечения с графиком функции .

В системе координат хОу построим график функции ). Для этого можно представить её в виде и, рассмотрев четыре возникающих случая, запишем эту функцию в виде

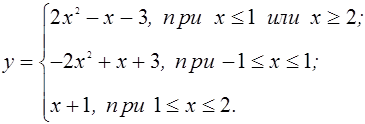
Поскольку график функции – это прямая, имеющая угол наклона к оси Ох, равный , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции . Поэтому находим производную

Ответ: .

III. Найти все значения параметра а, при каждом из которых система уравнений

имеет решения.

Решение.

Из первого уравнения системы получим при Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы “скользят” вершинами по оси абсцисс.

Выделим в левой части второго уравнения полные квадраты и разложим её на множители

Множеством точек плоскости , удовлетворяющих второму уравнению, являются две прямые

и

Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.

Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается

прямой ), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то .

Случай касания “полупараболы” с прямой определим из условия существования единственного решения системы

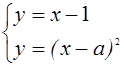
В этом случае уравнение

имеет один корень, откуда находим :