Реферат: Решение уравнений, неравенств, систем с параметром (алгебра и начала анализа)

Следовательно, исходная система не имеет решений при , а при или имеет хотя бы одно решение.

Ответ: а Î (-¥;-3] È(;+¥).

IV. Решить уравнение

Решение.

Использовав равенство , заданное уравнение перепишем в виде

Это уравнение равносильно системе

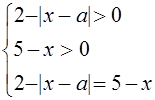
Уравнение перепишем в виде

. (*)

Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций и Из графика следует, что при графики не пересекаются и, следовательно, уравнение не имеет решений.

Если , то при графики функций совпадают и, следовательно, все значения являются решениями уравнения (*).

При графики пересекаются в одной точке, абсцисса которой 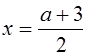. Таким образом, при уравнение (*) имеет единственное решение - .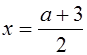

Исследуем теперь, при каких значениях а найденные решения уравнения (*) будут удовлетворять условиям

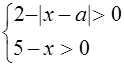
Пусть , тогда . Система примет вид

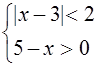
Её решением будет промежуток хÎ (1;5). Учитывая, что , можно заключить, что при исходному уравнению удовлетворяют все значения х из промежутка [3; 5).

Рассмотрим случай, когда 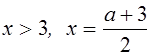. Система неравенств примет вид

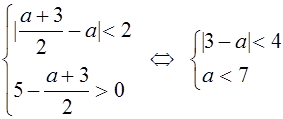
Решив эту систему, найдем аÎ (-1;7). Но , поэтому при аÎ (3;7) исходное уравнение имеет единственное решение .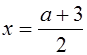

Ответ:

если аÎ (-¥;3), то решений нет;

если а=3, то хÎ [3;5);

если aÎ (3;7), то ;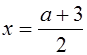

если aÎ [7;+¥), то решений нет.

V. Решить уравнение

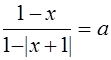, где а - параметр. (5)