Реферат: Решение уравнений, неравенств, систем с параметром (алгебра и начала анализа)

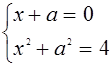
а значения и находятся из системы

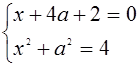
Решая эти системы, получаем, что

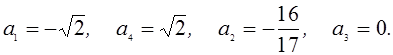
Ответ:

III. Решить неравенство на в зависимости от значений параметра а.

Решение.

Находим область допустимых значений –

Построим график функции в системе координат хОу.

при неравенство решений не имеет.

при для решение х удовлетворяет соотношению , где

Ответ: Решения неравенства существуют при

, где , причем при решения ; при решения .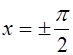

IV. Решить неравенство

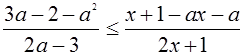
Решение.

Находим ОДЗ или линии разрыва (асимптоты)

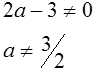
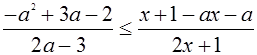
Найдем уравнения функций, графики которых нужно построить в ПСК; для чего перейдем к равенству :

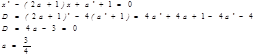
Разложим числитель на множители.

т. к. то

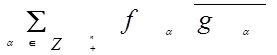
Разделим обе части равенства на при . Но является решением : левая часть уравнения равна правой части и равна нулю при .
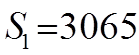