Реферат: Решение уравнений, неравенств, систем с параметром (алгебра и начала анализа)
При любом а : ![]()
Если ![]() , то
, то 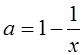 ;
;
если ![]() , то
, то  .
.
Строим график функции  , выделяем ту его часть , которая соответствует
, выделяем ту его часть , которая соответствует ![]() . Затем отметим ту часть графика функции
. Затем отметим ту часть графика функции  , которая соответствует
, которая соответствует ![]() .
.
По графику определяем, при каких значениях а уравнение (5) имеет решение и при каких – не имеет решения.
Ответ:
если ![]() , то
, то 

если ![]() , то
, то  ;
;
если ![]() , то решений нет;
, то решений нет;
если ![]() , то
, то  ,
,  .
.
VI. Каким условиям должны удовлетворять те значения параметров ![]() и
и ![]() , при которых системы
, при которых системы
 (1)
(1)
и
 (2)
(2)
имеют одинаковое число решений ?
Решение.
С учетом того, что ![]() имеет смысл только при
имеет смысл только при ![]() , получаем после преобразований систему
, получаем после преобразований систему
 (3)
(3)
равносильную системе (1).
Система (2) равносильна системе
 (4)
(4)
Первое уравнение системы (4) задает в плоскости хОу семейство прямых, второе уравнение задает семейство концентрических окружностей с центром в точке А(1;1) и радиусом ![]()
Поскольку ![]() , а
, а ![]() , то
, то ![]() , и, следовательно, система (4) имеет не менее четырех решений. При
, и, следовательно, система (4) имеет не менее четырех решений. При ![]() окружность касается прямой
окружность касается прямой ![]() и система (4) имеет пять решений.
и система (4) имеет пять решений.
Таким образом, если ![]() , то система (4) имеет четыре решения, если
, то система (4) имеет четыре решения, если ![]() , то таких решений будет больше, чем четыре.
, то таких решений будет больше, чем четыре.
Если же иметь в виду не радиусы окружностей, а сам параметр а, то система (4) имеет четыре решения в случае, когда ![]() , и больше четырех решений, если
, и больше четырех решений, если ![]() .
.
Обратимся теперь к рассмотрению системы (3). Первое уравнение этой системы задаёт в плоскости хОу семейство гипербол, расположенных в первом и втором квадрантах. Второе уравнение системы (3) задает в плоскости хОу семейство прямых.
При фиксированных положительных а и b система (3) может иметь два, три, или четыре решения. Число же решений зависит от того, будет ли прямая, заданная уравнением ![]() , иметь общие точки с гиперболой
, иметь общие точки с гиперболой ![]() при
при ![]() (прямая
(прямая ![]() всегда имеет одну точку пересечения с графиком функции
всегда имеет одну точку пересечения с графиком функции ![]() ).
).
Для решения этого рассмотрим уравнение
![]() ,
,