Реферат: Розрахунки надійності електронної апаратури
Для характеристики точності та надійності оцінки ![]() користуються так званим довірчим інтервалом і довірчою ймовірністю. Нехай для параметра v отримана з п дослідів незсунена оцінка
користуються так званим довірчим інтервалом і довірчою ймовірністю. Нехай для параметра v отримана з п дослідів незсунена оцінка ![]() . Оцінімо ймовірність, при якій допущена помилка не перевищить деякої величини ε. Позначимо цю ймовірність:
. Оцінімо ймовірність, при якій допущена помилка не перевищить деякої величини ε. Позначимо цю ймовірність:
![]() (8)
(8)
Це є ймовірність того, що справжнє (дійсне) значення v міститиметься в межах ![]()
Ймовірність Р(ε) називається довірчою ймовірністю, межі (границі) ![]() довірчими межами (границями), інтервали Іε=
довірчими межами (границями), інтервали Іε=![]() ±ε – довірчими інтервалами.
±ε – довірчими інтервалами.
Довірчий інтервал характеризує точність отриманого результату, а довірча ймовірність – його надійність.
2.1 Довірчий інтервал при нормальному розподілі
Нехай величина Х розподілена за нормальним законом з параметрами Мх і σх . Розглянемо питання про знаходження довірчих границь для математичного сподівання.
Потрібно знайти ймовірність нерівності:
![]() (9)
(9)
Якби закон розподілу ![]() був відомим, то знаходження ймовірності нерівності (9) не викликало б складнощів. Проте закон розподілу оцінки
був відомим, то знаходження ймовірності нерівності (9) не викликало б складнощів. Проте закон розподілу оцінки ![]() залежить від розподілу величини Х та її невідомих параметрів Мх і σх .
залежить від розподілу величини Х та її невідомих параметрів Мх і σх .
Нам відомо, що величина Х розподілена за нормальним законом, але зважаючи на те, що параметри Мх і σх цього закону невідомі, скористуватися цим законом розподілу неможливо.
Щоб обійти це ускладнення, введемо замість випадкової величини ![]() іншу випадкову величину Тт :
іншу випадкову величину Тт :
 (10)
(10)
де  (11)
(11)
п – кількість спостережень;
![]() – статистична дисперсія величини Х.
– статистична дисперсія величини Х.
В математичній статистиці доведено, що випадкова величина Тт підкоряється так званому закону Стьюдента:
 (12)
(12)
де Г(п/2) – гамма – функція;
п – кількість спостережень.
З рівняння (12) видно, що розподіл Стьюдента не залежить від параметрів Мх і σх величини Х, а залежить тільки від аргументу t і кількості спостережень п.
Розподіл Стьюдента дозволяє знайти ймовірність нерівності ![]() Для цього задамося довільним позитивним числом ta і знайдемо ймовірність влучення величини Тт на відрізок (-ta , ta ):
Для цього задамося довільним позитивним числом ta і знайдемо ймовірність влучення величини Тт на відрізок (-ta , ta ):
 (13)
(13)
Підставимо в ліву частину цієї формули замість Тт його значення з формули (10) і отримаємо:
 (14)
(14)
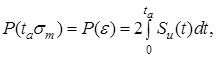 (15)
(15)
де ![]() – довірча ймовірність;
– довірча ймовірність;
![]()
ta – квантиль розподілу Стьюдента для вибраної ймовірності P(ε) та кількості ступенів свободи r=n-1.