Реферат: Розрахунки надійності електронної апаратури

На практиці часто потребується отримати в процесі випробування інтенсивність відмов з помилкою, яка б не перебільшувала задану. В цьому випадку при плануванні випробовувань потрібно визначити кількість відмов п, кількість екземплярів апаратури N, яку поставили на випробовування, сумарне напрацювання апаратури t_Σ та довжину етапу випробовувань t_в .

Якщо задана гранична помилка виражена у відсотках і дорівнює ξ_о , то:

(23)

Для експоненціального розподілу часу безвідмовної роботи:

Тоді, при заданій ймовірності Р() і r_ξ =r₁ визначимо кількість відмов п, яку необхідно отримати в процесі випробовувань. Об’єм вибірки за виразом (18). Результати випробовувань вважаються позитивними, якщо:

(24)

2.3 Довірчий інтервал при розподілі Пуассона

надійність електроапаратура експоненціальний

Довірчі границі у випадку розподілу Пуассона обчислюється за формулами :

; (25)

де а – параметр розподілу Пуассона (математичне сподівання кількості відмов); а = λt;

n – кількість відмов, які виникли в процесі випробовування;

коефіцієнти r₁ і r₂ визначаються за формулою (21).

Довірчий інтервал для інтенсивності відмов при розподілі Пуассона знаходиться так:

1. Задаємося довірчою ймовірністю Р(ε).

2. За заданими значеннями п та Р(ε) знаходимо коефіцієнти r₁ і r₂ .

3. Розраховуємо за формулою (25) значення а_н та а_в параметрів розподілу Пуассона.

4. За заданим сумарним напрацюванням t_Σ знаходимо довірчі границі для λ:

3. Критерії згоди

Між статистичним розподілом та теоретичною кривою на практиці завжди є розбіжності. При цьому потрібно переконатися, викликані ці розбіжності тільки випадковими обставинами, які пов’язані з обмеженою кількістю спостережень, або вони є істотні і пов’язані з тим, що вибрана крива погано вирівнює даний статистичний розподіл. Отже, виникає питання про узгодження теоретичного і статистичного розподілів. Перевірка такої узгодженості здійснюється за критеріями згоди. Критеріями, які найбільш використовуються, є критерій Колмогорова та критерій χ² Пірсона.

3.1 Критерій Колмогорова

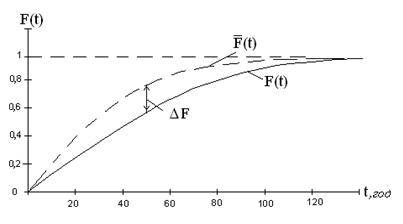
При застосуванні критерію згоди Колмогорова як захід розбіжності між теоретичним і статистичним розподілом розглядається максимальне значення модуля різниці між теоретичною та експоненціальною функціями розподілу.

На рис. 2 наведені теоретична та експоненціальна функції розподілу F(t).