Реферат: Сборник Лекций 2 по Мат.Анализу
df(x0,y0) = fx(х0,у0)x + fу(х0,у0)у. (2)
Если точка, в которой вычисляется дифференциал не существенна, его принято обозначать просто df. Из определения следует, что дифференциал представляет собой главную часть приращения функции, линейную относительно приращений её аргументов. Полагая поочерёдно f(x,y) = х и f(x,y) = у, получим, что дифференциалы dх и dy независимых аргументов функции х и у равны соответственно x и у . Таким образом
df = fx dх + fу dу.
Раньше говорилось о том, что из существования частных производных в точке не следует непрерывности функции в этой точке. Однако, из справедливости равенства (1) следует
![]() ,
,
а это означает непрерывность функции в точке (х0,у0). Следовательно, дифференцируемая в точке функция обязательно непрерывна в этой точке.
Из сказанного следует, что существование обеих частных производных функции в точке не означает, что функция дифференцируема в этой точке. В курсе математического анализа доказывается теорема, что функция дифференцируема в точке, если обе частные производные этой функции непрерывны в этой точке.
На рисунке 1 график функции z = f(x,y) представляет собой поверхность F. Длина отрезка Р0Р равна значению функции z в точке P0,
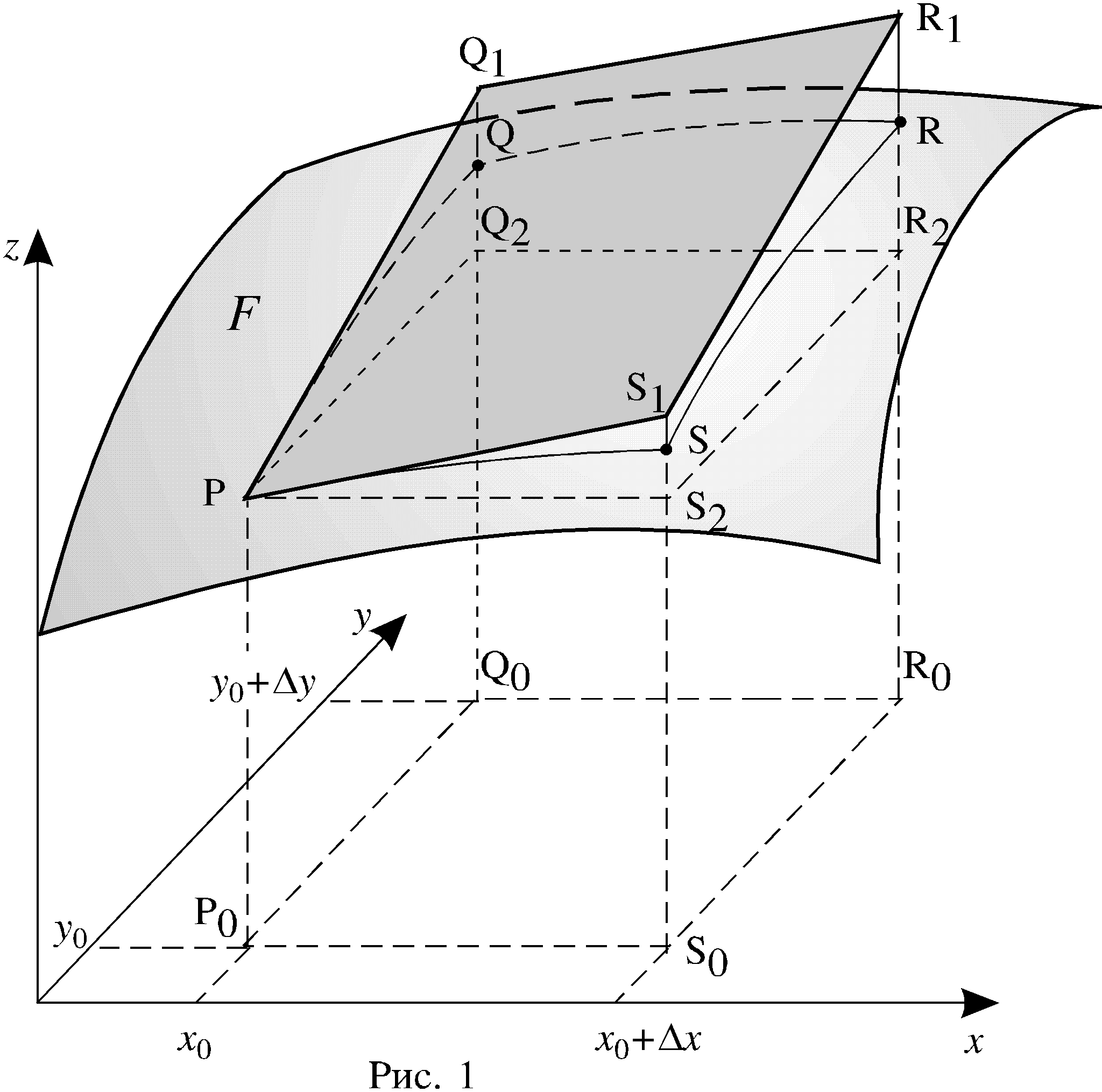
?? ???? ?0??=?f(x0,y0) (?? ??????? ??? ??????????? ??????????? F ??????? ???, ??? ??? ??????????????? ???????? ??????? ? ?????????? ? ????? P0 ????????????, ?? ??? ?? ???????????? ?????????????? ??????????? ???? ??????? ? ?????? ? ????? ??????). ???????????? ????? Q0, S0 ? R0 ???????? ???? ????? ?????????????? (x0,y0+у); (x0+x,y0) ? (x0+x,y0+у), ?????? Q0Q?=?f(Q0), S0S?=?f(S0) ? R0R?=?f(R0). ?????????? f(х0,у0)???????? ? ????? ?0 ????? RR2.
Параллелограмм PQ1R1S1 лежит в плоскости, которая касается поверхности F в точке Р. Прямоугольник PQ2R2S2 расположен в горизонтальной плоскости. Очевидно: Q2Q1 = fy(x0,y0)y и S2S1 = fx(x0,y0)x.
Из легко доказываемого равенства
R2R1 = S2S1 + Q2Q1
и формулы (2) следует, что дифференциал функции в точке Р0 равен R2R1.
Так как df(x0,y0) f(x0,y0), дифференциал df даёт приближенное значение приращения функции при малых значениях приращений аргументов.
§4. Производная по направлению.
Пусть в плоскости XOY расположена точка M0(x0,y0). Зададим произвольный угол и рассмотрим множество точек на той же плоскости, координаты которых определяются из формул
x = x0 + t cos, y = y0 + t sin. (1)
Здесь t параметр, который может быть равен любому числу. Из формул (1) следует:
(y - y0)/(x - x0) = tg
Это означает, что все точки M(x,y), координаты которых удовлетворяют равенствам (1), лежат на прямой, проходящей через точку M0(x0,y0) и составляющей угол с осью OX. Каждому значению t соответствует единственная точка M(x,y), лежащая на этой прямой, причем согласно формуле (1) из §1 расстояние между точками M0(x0,y0) и M(x,y) равно t. Можно считать эту прямую числовой осью с положительным направлением, определяемым возрастанием параметра t. Обозначим положительное направление этой оси символом l.
Производной функции z = f(x,y) в точке M0(x0,y0) по направлению l называется число
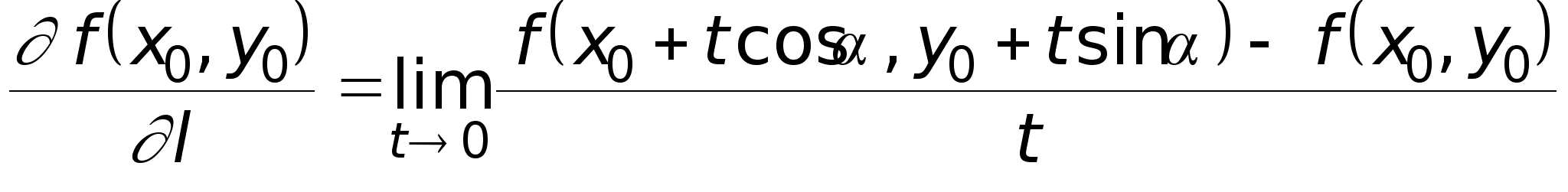 . (2)
. (2)
Производной функции по направлению можно дать геометрическую интерпретацию. Если через прямую l, определяемую формулами (1), провести вертикальную плоскость P (на самом деле в трехмерном пространстве уравнения (1) определяют эту самую плоскость), то эта плоскость пересечет поверхность-график функции z = f(x,y) вдоль
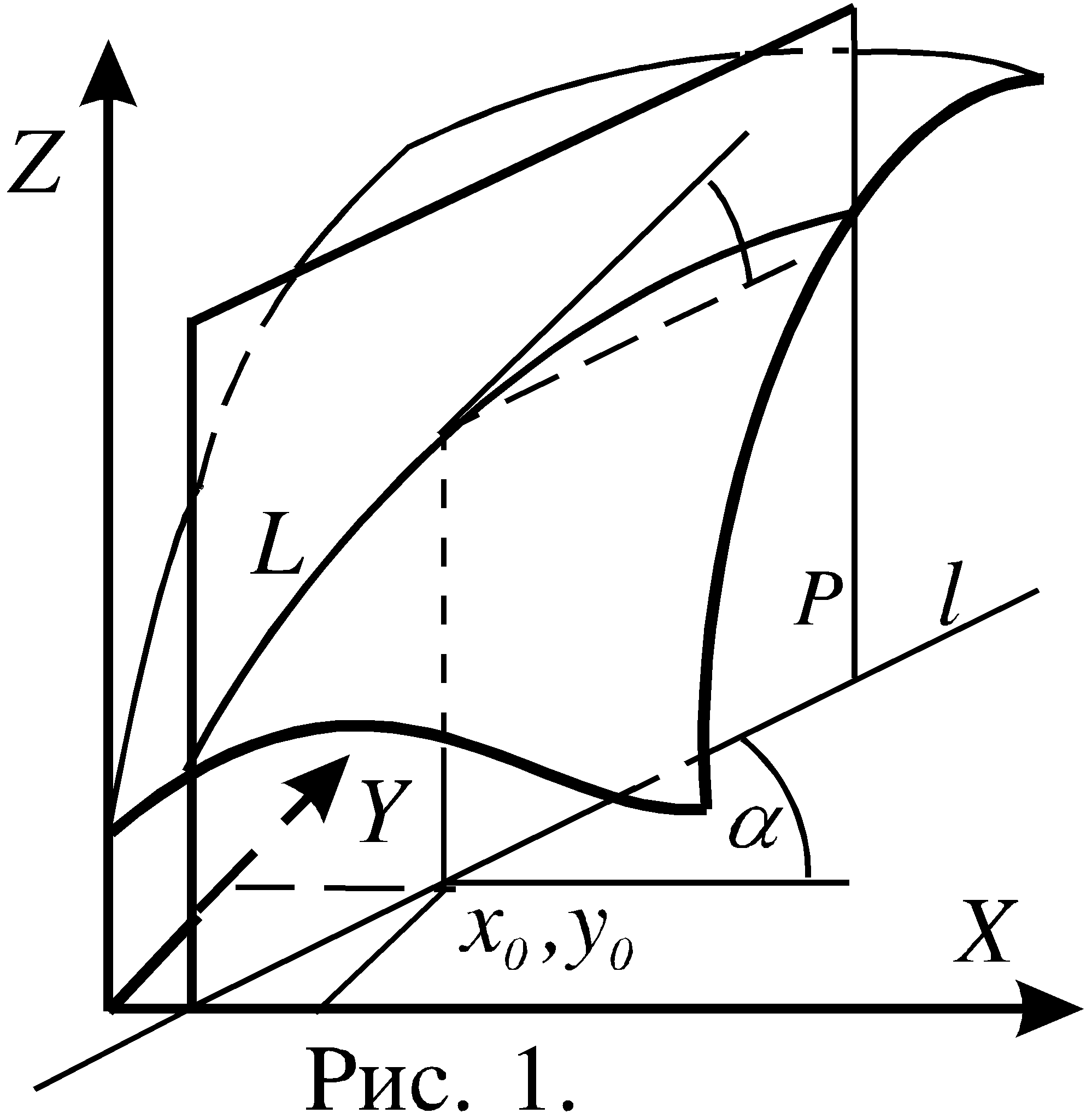
![]() В любом курсе математического анализа доказывается, что производная по направлению, определяемая формулой (2), может быть представлена в виде
В любом курсе математического анализа доказывается, что производная по направлению, определяемая формулой (2), может быть представлена в виде
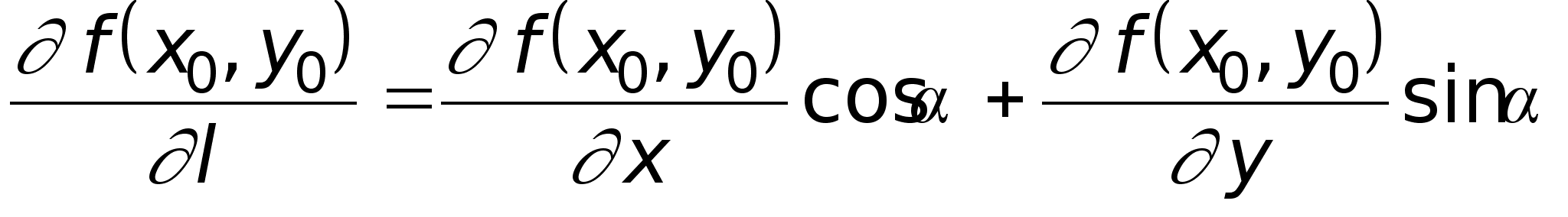 . (3)
. (3)