Реферат: Синтез системы автоматического регулирования массы квадратного метра бумажного полотна
Получаем:
![]() Þ К2 = 0
Þ К2 = 0
Найдем колебательную границу устойчивости, для этого подставим:
Р= j w
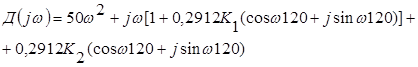
Тогда:

Решив уравнение относительно К1 и К2 , найдем выражение для колебательной границы устойчивости в виде:
![]()
![]()
Рассчитываем три точки колебательной границы устойчивости при w=0; Dw; 2Dw.
| w [ c -1 ] | 0 | 0,005 | 0,01 |
| К1 , | 3,434 | 3,3191 | 2,8446 |
|
К2 , | 0 | 0,0132 | 0,0382 |
СТУДЕНТ Ситников С.А. ГРУППА 2102
РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ (ЛИНИИ РАВНОГО ЗАПАСА УСТ.) НЕПРЕР.АСР
ПАРАМЕТРЫ МОДЕЛЕЙ ИЗВЕСТНОЙ ЧАСТИ СИСТЕМЫ
МОДЕЛЬ ОБЪЕКТА ПО КАНАЛУ УПРАВЛЕНИЯ :
коэффициент передачи объекта = 112.0000
постоянная времени объекта = 50.0000
запаздывание объекта = 120.0000
Коэф.передачи исполн.устройства = 1.0000
Коэф.передачи регулир.органа = 0.0104
Коэффициент передачи датчика = 0.2500
РАСЧЕТ ОБЛАСТИ УСТОЙЧИВОСТИ
АПЕРИОДИЧЕСКАЯ ГРАНИЦА УСТОЙЧИВОСТИ K2 = 0
ТАБЛИЦА КОЛЕБАТЕЛЬНОЙ ГРАНИЦЫ УСТОЙЧИВОСТИ
W K1 K2
0.000000 -3.434066 0.000000
0.001538 -3.327219 0.001369
0.003077 -3.011959 0.005329