Реферат: Складність методів вирішення проблеми дискретного логарифмування в групі точок еліптичної кривої

Знаходимо

Перевіряємо

Таким чином

Цей алгоритм при великих значеннях ![]() стає менш ефективним. Як показали дослідження, алгоритм можна поліпшити. Для цього точки еліптичної кривої розбивають на три множини та обчислюють функцію
стає менш ефективним. Як показали дослідження, алгоритм можна поліпшити. Для цього точки еліптичної кривої розбивають на три множини та обчислюють функцію ![]() рекурентно за правилом
рекурентно за правилом

де ![]() – випадкові цілі числа з інтервалу
– випадкові цілі числа з інтервалу ![]() .
.
Під час використання формул даного виду можна зменшити складність криптоаналізу. Крім того це дозволяє ефективно розпаралелити процес знаходження коефіцієнтів ![]() та
та ![]() , для яких виконується вимога
, для яких виконується вимога ![]() ,
, ![]() як мінімум на
як мінімум на ![]() процесів.
процесів.
Стійкість ![]() заснована на складності розв’язання задачі дискретного логарифмування. У порівнянні з більше ранніми прототипами - криптосистемами Діффі-Хеллмана й Ель-Гамала - вони дають істотний виграш у криптостійкості, або практично на порядок дозволяють скоротити розмір поля при порівняній стійкості. Відомо, що
заснована на складності розв’язання задачі дискретного логарифмування. У порівнянні з більше ранніми прототипами - криптосистемами Діффі-Хеллмана й Ель-Гамала - вони дають істотний виграш у криптостійкості, або практично на порядок дозволяють скоротити розмір поля при порівняній стійкості. Відомо, що ![]() порядку 160 біт порівнянний щодо безпеки з RSA і криптосистемою Eль-Гамала з розміром ключа 1024 біт, причому цей виграш прогресує зі збільшенням довжини ключа.
порядку 160 біт порівнянний щодо безпеки з RSA і криптосистемою Eль-Гамала з розміром ключа 1024 біт, причому цей виграш прогресує зі збільшенням довжини ключа.
Щоб оцінити складність ![]() (Elliptic Curve Discrete Logarithm Problem ), уявімо на хвилину, що піщина з лінійним розміром 0,1 мм є однією з точок ЕСС . Якої величини буде планета, складена з
(Elliptic Curve Discrete Logarithm Problem ), уявімо на хвилину, що піщина з лінійним розміром 0,1 мм є однією з точок ЕСС . Якої величини буде планета, складена з ![]() таких піщин? Якщо
таких піщин? Якщо ![]() -радіус планети в кілометрах, то
-радіус планети в кілометрах, то ![]() й
й ![]() км. Це приблизно в
км. Це приблизно в ![]() раз перевищує радіус нашої планети. Серед цього вражаючого числа піщин потрібно знайти одну. Це й буде розв’язком, порівнянним за складністю з
раз перевищує радіус нашої планети. Серед цього вражаючого числа піщин потрібно знайти одну. Це й буде розв’язком, порівнянним за складністю з ![]() для
для ![]() із числом точок порядку
із числом точок порядку ![]() .
.
Практично обчислювальна складність вимірюється в MIPS-роках (MIPS – Million Instructions per Second - мільйон інструкцій за секунду ). Під однією операцією тут розуміють одне додавання точок кривої. Оцінки часу рішення ![]() за допомогою
за допомогою ![]() -методу Полларда залежно від розміру поля й порядку
-методу Полларда залежно від розміру поля й порядку ![]() криптосистеми наведено в таблиці 2
криптосистеми наведено в таблиці 2
Проблема дискретного логарифмування на еліптичній кривій формулюється в такий спосіб: відома точка G криптосистеми простого порядку ![]() й точка
й точка ![]() Необхідно знайти ціле число
Необхідно знайти ціле число ![]()
Термінологія тут успадкована із класичної проблеми дискретного логарифмування (![]() ) у мультиплікативній групі поля криптосистеми розподілу ключів Діффі-Хеллмана, у якій однобічна функція
) у мультиплікативній групі поля криптосистеми розподілу ключів Діффі-Хеллмана, у якій однобічна функція ![]() експоненціювання елемента
експоненціювання елемента ![]() поля обчислюється швидко (у поліноміальному часі), а зворотна функція дискретного логарифмування
поля обчислюється швидко (у поліноміальному часі), а зворотна функція дискретного логарифмування ![]() - повільно (за експоненційний час). Суть цієї проблеми для
- повільно (за експоненційний час). Суть цієї проблеми для ![]() не міняється, якщо операцію множення замінити операцією додавання (в адитивній групі точок
не міняється, якщо операцію множення замінити операцією додавання (в адитивній групі точок ![]() ), при цьому експоненціювання переходить в
), при цьому експоненціювання переходить в ![]() -кратне додавання точок.
-кратне додавання точок.
Таблиця 2 - Складність і час обчислення рішення ECDLP за допомогою 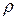 -методу Полларда залежно від порядку
-методу Полларда залежно від порядку 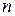 криптосистеми
криптосистеми
|
Розмір поля, Біт |
Порядок |
Складність
|
Час обчислень
|
|
163 |
160 |
|
|
|
191 |
186 |
|
К-во Просмотров: 313
Бесплатно скачать Реферат: Складність методів вирішення проблеми дискретного логарифмування в групі точок еліптичної кривої
|