Реферат: Складність методів вирішення проблеми дискретного логарифмування в групі точок еліптичної кривої

239

234

359

354

431

426

історично була визначена як адитивна група, але з тим же успіхом можна було б визначити як мультиплікативну, назвавши групову операцію множенням точок.

Операція експоненціювання у мультиплікативній групі найбільш ефективно здійснюється методом послідовного піднесення до квадрата. Для цього число подається у двійковій системі числення

як -розрядне двійкове число . Наприклад, мінімальним 5-розрядним числом (з 1 у старшому розряді) є двійкове число (рівне 16 у десятковій системі), а максимальним – число 11111 (рівне 31 у десятковій системі). Тоді експоненціювання елемента зводиться до послідовного піднесення до квадрата і множення на (останнє за наявності 1 у двійковому записі від старшого розряду до молодшого):

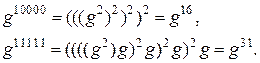
У першому випадку виконується 4 операції множення, у другому 8-множень. У загальному випадку експоненціювання у двійкову -розрядний степінь цим методом здійснюється за допомогою від до операцій множення за модулем . Об'єм обчислень пропорційний розрядності числа . Така обчислювальна складність називається поліноміальною а - коефіцієнт пропорційності ).

Зворотна функція дискретного логарифмування у найгіршому разі може зажадати перебору до значень, при цьому говорять про експонентну складність обчислень

Взагалі кажучи, поняття обчислювальної складності визначається через співвідношення вхідного й вихідного об'ємів даних деякого обчислювального алгоритму. Алгоритми поліноміального часу (швидкі алгоритми) характеризуються лінійним співвідношенням об'ємів даних на виході й вході процесора, а алгоритми експонентного часу (повільні), відповідно, експонентним. Зі збільшенням об'єму вхідних даних експонентна складність веде до практично нереалізованих обчислювальних витрат.

Сьогодні відомі досить ефективні субекспоненційні методи рішення DLP над скінченними полями. Це пов'язано з тим, що елемент поля - ціле число, яке можна факторизувати у вигляді добутку ступенів простих чисел. Це затребувано з метою безпеки істотно збільшити розміри поля для криптосистем Діффі-Хеллмана й Ель-Гамала (до тисяч біт). З іншого боку, точку еліптичної кривої факторизувати на зразок цілого числа не вдається. Тому для ЕСС поки не відомі методи розв’язання , більш ефективні, ніж класичні методи з експонентною складністю обчислень. Цим і пояснюється високий рівень безпеки криптосистем на еліптичних кривих.

Криптоатаки на прийнято розділяти на дві групи: атаки на загальну структуру й атаки ізоморфізму. До першого звичайно відносять:

– метод Шенкса( Shenks Method- Giant Step-Baby step);

– методи Полларда (Pollard¢s Method);

– метод Поліга- Хеллмана (Pohlig-Hellman Method);

– метод обчислення степенів (Index Calculus Method).

Ці методи застосовні для будь-якої скінченної групи, у тому числі й для еліптичної кривої (крім останнього). Атаки ізоморфізму специфічні для ECC. Серед них найбільш відомі:

– атака Менезиса, Окамото й Ванстоуна, або MOV- атака;

– ізоморфізм Семаєва;